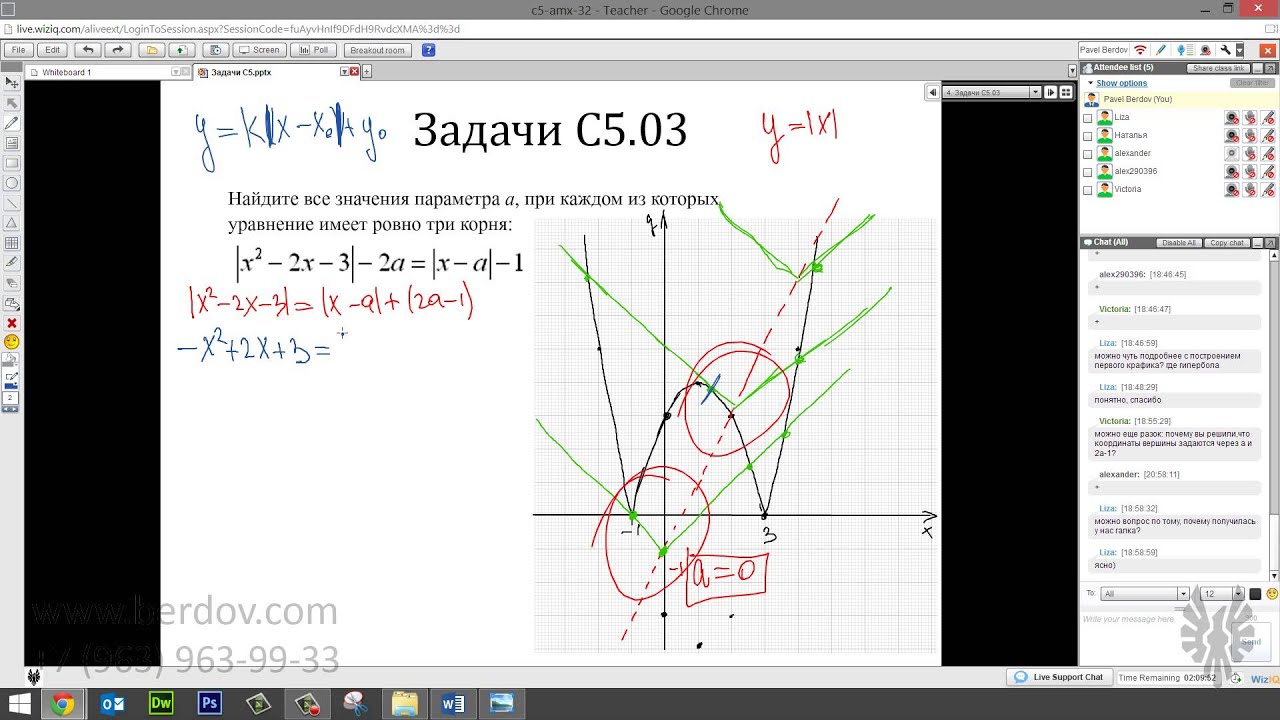
Сегодня мы разберём задачу с параметром, содержащую модуль, которая в итоге решается и с применением аналитических методов. и графически. Это так называемые комбинированные задачи — они не очень сложны, но при невнимательной работе весьма коварны.:)

Оригинал урока:
http://www.berdov.com/docs/par....ametr/grafik-modulya

Оригинал взят отсюда:
http://www.berdov.com/ege/para....metr/parametr-grafic

Математика — это просто. Приходите на занятия и убедитесь в этом сами: http://www.berdov.com

http://www.berdov.com/ege/para....metr/uravnenie-okruj

В этом видеоуроке репетитор по математике Павел Бердов решает реальную задачу C5 из ЕГЭ по математике с подробным объяснением каждого шага. Кроме того, в задаче присутствует сразу несколько «подводных камней», на которые обращается отдельное внимание.

http://www.berdov.com/ege/para....metr/okrujnost-modul

Это реальная задача C5 из ЕГЭ по математике, которая решается очень легко, если знать парочку приемов работы с графиками функций. В противном случае решение оказывается крайне сложным и проблематичным.

http://www.berdov.com/ege/para....metr/okrujnost-modul
Это одна из тех задач С5, которые, во-первых, действительно могут встретиться на ЕГЭ по математике. А во-вторых, многие ученики считают такие задачи чересчур сложными. В частности, из-за того, что в системе уравнений присутствует сразу два параметра.
Однако если вы посмотрите это видео, то лично убедитесь: при графическом подходе решать задачи с двумя параметрами оказывается очень и очень просто. Поэтому смело берите на вооружение данный прием и сдавайте ЕГЭ по математике на «отлично».

Иногда в задании 13 ЕГЭ по математике встречается такое тригонометрическое уравнение, которое нельзя решить напролом — сведением к sin x = a. Тогда к делу подключаются нестандартные приёмы:
1. Оценка левой и правой части (метод мажорант);
2. Исследование возрастания/убывания функции;
3. Разложение на множители и т.д.

Но сегодня не об этом. Сегодня мы попробуем решить эту задачу стандартными методами алгебры, которые работают не только в тригонометрии, но именно в тригонометрии они дают неожиданные результаты. О чём именно пойдёт речь? Смотрите видео — и обязательно берите на вооружение.:)

00:03 Краткая вводная: основная идея решения
05:10 Задание 13
10:40 Пункт А — решаем уравнение
17:07 Пункт Б — отбираем корни
25:04 Заключение: ещё раз о главной идее решения

Рациональное — это логически обоснованное, теоретически осознанное, систематизированное универсальное.
Иррациональное -- находящееся за пределами разума, нелогичное, несоизмеримое с рациональным мышлением и противоречащее ему.
Технология -- не просто деятельность с использованием технических средств, а рационально организованный способ деятельности человека, посредством применения на практике знаний в любой области действительности, характеризующийся последовательностью, единством целей, средств и результата.

Основная страница вебинара:
https://www.berdov.com/webinar..../equation-root/10-09

Записаться на вебинар можно на сайте:
http://www.berdov.com/webinar/....equation-root/trigon

В ближайшее воскресенье, 9 октября, состоится вебинар по задачам 13 (тригонометрические уравнения и отбор корней). Сегодня — первое видео в рамках подготовки к предстоящему вебинару.:)

Обычно при решении тригонометрических уравнений получаются красивые корни и табличные значения. Но что делать, если получился какой-нибудь арктангенс? Как в этом случае грамотно отобрать корни на отрезке и не допустить обидных ошибок?

0:00 Описание проблемы: сложные тригонометрические уравнения в ЕГЭ по математике
0:41 Решение сложной задачи 13 из профильного ЕГЭ
2:24 Учёт области определения корня и тангенса
12:41 Как отмечать арктангенсы на тригонометрической окружности
14:47 Отбор корней уравнения на указанном отрезке
21:48 Проверка правильности решения
27:17 Ключевые выводы и факты

http://www.berdov.com/ege/equa....tion-root/arktangens

Решение тригонометрического уравнения в задаче 13 из профильного ЕГЭ по математике 2016. Отбор корней на отрезке графическим методом. Учимся применять формулы тригонометрии (синус двойного угла), а также используем замену переменной. Типичная задача из ЕГЭ.

0:00 Вступление, описание тригонометрических уравнений в ЕГЭ
по математике
0:34 Решение тригонометрической задачи из профильного ЕГЭ
2:20 Отбор корней уравнения на указанном отрезке
10:17 Заключение и рекомендации для учеников

http://www.berdov.com/ege/equa....tion-root/reshenie-u

Решение тригонометрических уравнений из ЕГЭ по математике 2016. Отбор корней на отрезке. Формула понижения степени в тригонометрии и её применение для решения уравнений.

0:00 Введение. Общие принципы решения тригонометрических уравнений с ограничением;
16:02 — Пример решения 1-го уравнения с корнем;
38:30 — Ещё один пример — более простой;
48:26 — Формула понижения степени в тригонометрическом уравнении;
59:36 — Заключение и повторение основных формул.

Оригинал урока:
http://www.berdov.com/docs/tri....gonometriya/uchet-og

Как решать показательные неравенства? Существует несколько методов — от простейших конструкций до всевозможных группировок и разложения на множители. Сегодня мы познакомимся с основными способами решения показательных неравенств и формулами преобразований.

Основной урок:
https://www.berdov.com/docs/ex....ponenta/reshenie-pok

В этом уроке мы продолжаем учиться решать логарифмические неравенства методом рационализации с привлечением других приёмов.

Оригинал видео:
http://www.berdov.com/docs/log....arithm/reshenie-loga

Метод математической индукции — это приём доказательства утверждений, зависящих от натурального параметра. Он состоит из трёх шагов:
1. Доказать утверждение для конкретных n. Например, для n = 1 или n = 2;
2. Предположить, что утверждение верно для n = k;
3. На основе этого предположения доказать, что утверждение верно для n = k + 1.

Если все три шага выполнены, то исходное утверждение будет доказано для всех натуральных чисел n. Это позволяет доказывать сложные и нестандартные формулы.

Сегодня мы будем тренироваться в применении метода мат. индукции на четырёх задачах: два равенства и два неравенства. Заодно повторим несколько важных фактов из теории тождеств и, собственно, неравенств.

00:00 Метод математической индукции на примере простой задачи
04:16 Более сложная задача, анализ формулы последнего слагаемого
08:17 Доказательство рациональных неравенств (больная тема для многих)
12:49 Доказательство иррациональных неравенств (вспоминаем квадратные корни)

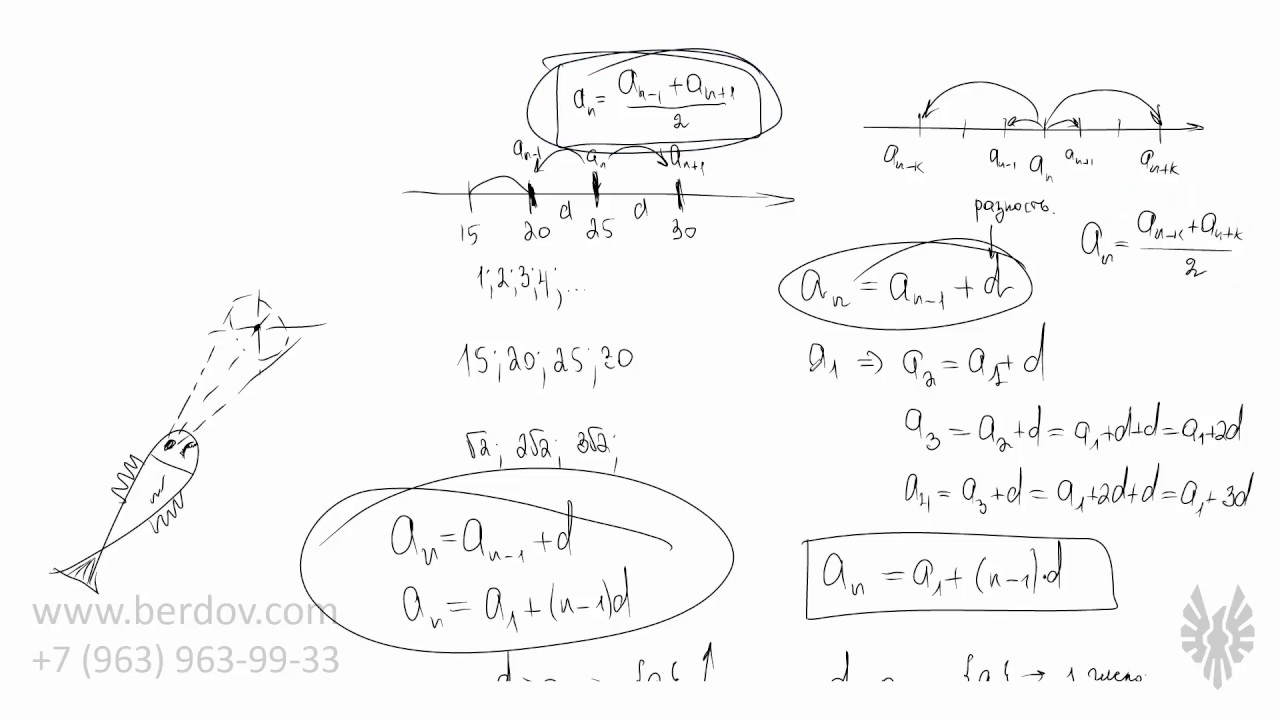
Это самый первый и самый важный урок по прогрессиям. Разбираем, что такое арифметическая прогрессия, какие у неё свойства, а заодно решаем кучу задач по прогрессиям.

Основная страница урока — там вы можете скачать задачи для самостоятельного решения и проверить себя:
https://www.berdov.com/docs/pr....ogressiya/chto-takoe

Более сложная версия предыдущей задачи — здесь требуется найти суммарные выплаты в течение второго года. Это одна из экономических задач 17 в ЕГЭ по математике 2016. Решается с помощью формул арифметической прогрессии.

Оригинал видео:
http://www.berdov.com/ege/cred....it/kredit-plyus-proc

Решение задач на арифметическую прогрессию. Вычисление n-го элемента арифметической прогрессии. Использование формул, первого элемента и разности прогрессии.

http://www.berdov.com/docs/pro....gressiya/prosteyshie

В этом видео мы познакомимся с новым объектом — арифметической прогрессией. Что такое арифметическая прогрессия? И как с ней работать. Как складывать её элементы и какие формулы для этого существуют? Об этом и поговорим.:)

Оригинал урока:
http://www.berdov.com/docs/pro....gressiya/chto-takoe-