Внешний угол треугольника больше любого внутреннего, с ним не смежного.

Рассмотрим треугольник АВС и какой-либо из его внешних углов, например угол, смежный с углом АСВ. Докажем, что он больше угла CВA.

Проведем медиану АD и продолжим ее за точку D на такое же рас­стояние. Получим точку A1.

Треугольник DСА1 равен треугольнику DBА (по первому при­знаку), откуда DBА = DСА1. Но угол DСА1 меньше угла, смежного с углом АСВ, поскольку составляет его часть.

Два прямоугольных треугольника равны, если гипотенуза и ка­тет одного треугольника соответственно равны гипотенузе и катету другого.

Кроме того, из первого признака равенства треугольников сле­дует равенство прямоугольных треугольников по двум катетам.

Прямоугольным называется треугольник, у которого есть прямой угол.

Стороны, заключающие прямой угол прямоугольного треугольни­ка, называются катетами прямоугольного треугольника.

Сторона, противоположная прямому углу, называется гипотену­зой прямоугольного треугольника.

Треугольник, как правило, задается тремя элементами.

Пусть в треугольниках ABC и А1В1С1 имеют место равенства АВ = А1В1, AС = A1С1, АВС = А1В1С1.

Обязательно ли такие треугольники равны?

Для того чтобы доказать, что такие треугольники могут быть и неравными, достаточно «предъявить» два неравных треугольника, у которых равны указан­ные в условии элементы. Как говорят математики, построить опро­вергающий пример.

Рассмотрим на плоскости какой-нибудь острый угол, вершину которого обозначим буквой В.

Возьмем на одной из его сторон точку А и с центром в этой точке нарисуем окруж­ность, которая пересекает другую сторону угла в двух точках. Обо­значим эти точки через С и С1.

Один из двух получившихся тре­угольников — это АВС, а другой — АВС1 (можно считать, что точки А и A1, В и В1 совпадают).

Как видим, эти треугольники не равны, хотя и удовлетворяют всем условиям нашей задачи.

Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Пусть для треугольников ABC и А1В1С1 имеют место равенства:
АВ равно А1В1,
ВС равно В1С1,
СА равно C1A1.

Рассмотрим две окружности с центрами в A и B и радиусами со­ответственно AC и BC. Эти окружности пересекаются в двух симмет­ричных относительно AB точках: C и С2.

Перене­сем треугольник А1В1С1 так, чтобы сторона А1В1 совпала со сторо­ной АВ, при этом должны совпасть вершины А1 и A, В1 и B.

Точка С1 после пе­реноса указанным образом треугольника А1В1С1 должна совпасть либо с точкой C, либо с точкой С2. В обоих случаях это будет означать равенство треугольников ABC и А1В1С1, поскольку треугольни­ки ABC и ABС2 равны, так как эти треугольники симметричны относитель­но прямой AB.

Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней уг­лам другого треугольника, то такие треугольники равны.

Пусть в треугольниках АВС и А1В1С1 имеют ме­сто равенства ВС = В1С1, АВС = А1В1С1, а АСВ = А1С1В1.

Наложим тре­угольник А1В1С1 на треугольник АВС так, чтобы совпали стороны ВС и В1С1 и прилегающие к ним углы.

При необходимости треугольник А1В1С1 можно «перевернуть обратной стороной».

Тогда треугольники совпадут полностью. Значит, они равны.

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого тре­угольника, то такие треугольники равны.

Рассмотрим два треугольника ABC и A1B1C1. Пусть в этих треугольниках равны стороны AB и A1B1, AC и A1C1, а угол BAC равен углу B1A1C1.

Тогда треугольник A1B1C1 можно наложить на треугольник ABC так, чтобы угол B1A1C1 совпал с углом BAC. При этом можно расположить треугольник A1B1C1 так, чтобы сторона А1В1 совпала со стороной АВ, а сторона А1С1 — со сторо­ной АС.

В случае необходимости вместо треугольника А1В1С1 можно рассматривать равный ему «перевернутый» треугольник, т.е. тре­угольник, симметричный А1В1С1 относительно произвольной прямой.

Тогда треугольники совпадут полностью, поскольку совпадут все их вершины.

Равные фигуры — это такие фигуры, которые можно совместить друг с другом, наложить друг на друга так, чтобы они совпали.

Как все же можно установить равенство двух фигур?

Равенство каких элементов — отрезков, углов или чего-то иного — обеспечивает и равенст­во самих фигур?

Мы знаем, что два отрезка равны, если равны их длины.

Из ра­венства радиусов следует и равенство окружностей.

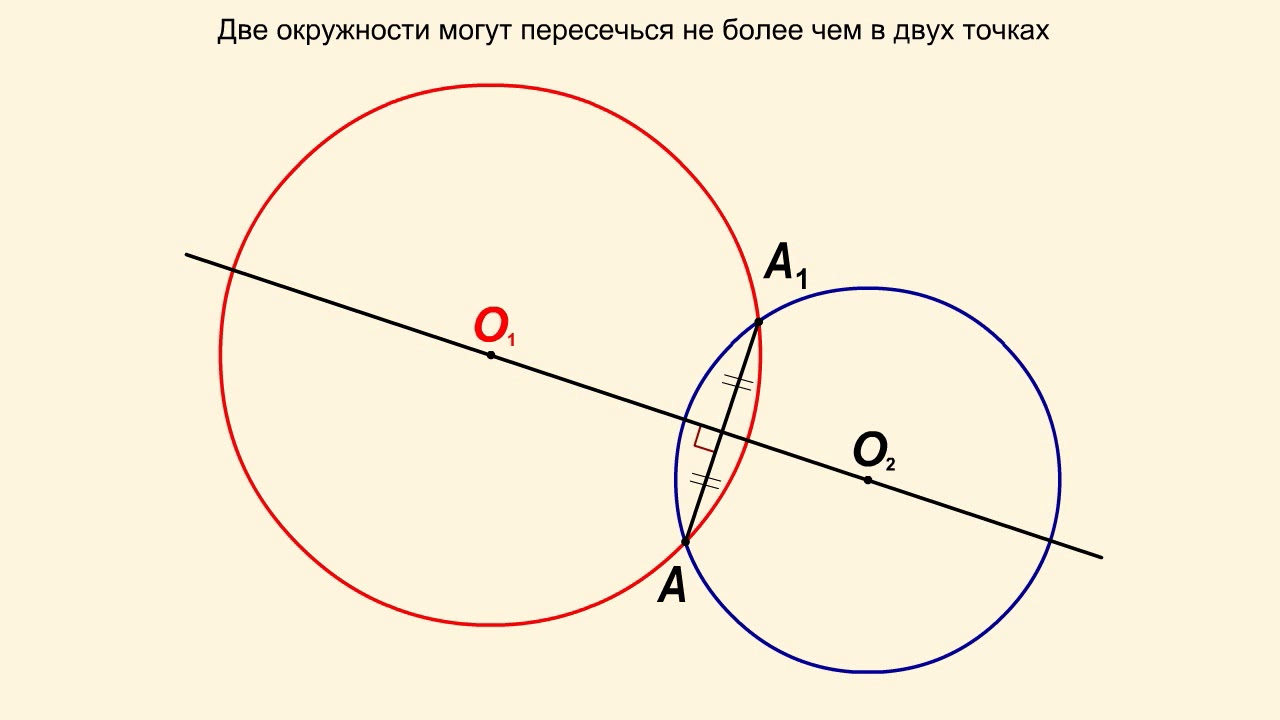
Рас­смотрим две пересекающиеся окружности с центрами O1 и O2. Пусть A — какая-то из точек пересечения этих двух окруж­ностей, не лежащая на прямой O1O2. Если точек пересечения более одной, то такая точка А найдется. Зафиксируем эту точку. Мы утвер­ждаем, что помимо точки A окружности могут пересечься еще в единственной точке, симметричной А относительно прямой O1O2.

В самом деле, пусть A1 — какая-то точка пересечения окружно­стей, отличная от A. Прямая, проходящая через O1 перпендикуляр­но AA1, делит AA1 пополам. Это следует из теоремы о диаметре перпендикулярном хорде, ведь AA1 — хорда окружности с центром O1. Точно так же пополам делит AA1 прямая, проходящая через O2 перпендикулярно AA1. Значит, эти два перпендикуляра совпадают с прямой O1O2, т.е. мы доказали, что A1 симметрична A относительно прямой O1O2. Таким образом, чис­ло точек пересечения двух окружностей не более двух.

Рассмотрим случай пересекающихся окружности и прямой.

Если прямая проходит через центр окружности, то наше утвер­ждение вполне очевидно. На прямой имеется ровно две точки, уда­ленные от данной точки этой прямой на определенное расстояние.

Рассмотрим теперь общий случай. Пусть окружность с центром О пересекается с прямой а в точке А. Опустим из О перпен­дикуляр b на прямую а. Если A1 — еще одна точка пересечения прямой а с окружностью, то треугольник AOA1 является равнобедрен­ным с основанием AA1. По свойству равнобедренных треугольников перпендикуляр b делит отрезок AA1 пополам, или, иначе, A1 симметрична А относительно b. Это означает, что, помимо точки A, прямая а может пересечься с окружностью не более чем еще в одной точке.

Теорема о равнобедренном треугольнике имеет непосредствен­ное отношение к свойствам окружности. Ведь любую хорду окружности можно рассматривать как основание равнобедренного тре­угольника, противоположная вершина которого расположена в центре окружности. Этот прием часто используется при доказатель­стве различных свойств окружности и решении задач.

Свойство хорд окружности можно сформулировать так: «Перпендикуляр, опущенный из центра окружности на хорду этой окружности, делит хорду пополам».

Это же можно выразить несколько иначе: «Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам».

Рассмотрим тре­угольник OPK, где PK — некоторая хорда окружности, а О — центр.

Этот треугольник равнобедренный: OP = OK. Теперь мы мо­жем воспользоваться свойством равнобедренных треугольников, по которому медиана, биссектриса и высота, проведенные к основа­нию, совпадают. Значит, перпендикуляр, опущенный из вершины О на PK, делит PK пополам.

В любом равнобедренном треугольнике:

- углы при основании равны;
- медиана, биссектриса и высота, проведенные к основа­нию, совпадают.

Оба эти свойства доказываются совершенно одинаково. Рассмотрим равнобедренный треугольник АВС, в кото­ром АВ = ВС.

Пусть ВВ1 — биссектриса этого треугольника. Как известно, прямая BB1 является осью симметрии угла АВС.

Но в силу равенства AB = BC при этой симметрии точка А переходит в С. Следовательно, треугольники ABB1 и CBB1 равны.

Отсюда все и сле­дует. Ведь в равных фигурах равны все соответствующие элементы. Значит, угол BAB1 = угол BCB1.

Кроме того, AB1= CB1, т.е. BB1 — медиана и угол BB1A = угол BB1C = 90°; таким образом, BB1 также и высота треугольника ABC.

Равносторонний треугольник — треугольник, у которого все стороны равны.

Если у треугольника равны все три стороны, то он называется равносторонним.

Равнобедренный треугольник — треугольник, у которого две стороны равны.

Треугольник с двумя равными сторонами называется равнобедренным, при этом равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.

С каждым треугольником связан ряд отрезков и линий, имеющих специальные названия.

Отрезок прямой, соединяющий какую-либо вершину треугольника с серединой противоположной стороны, называется медианой тре­угольника.

Отрезок биссектрисы угла треугольника от вершины до точки пе­ресечения со стороной треуголь­ника называется биссектрисой тре­угольника.

Проведем через вершину треугольника прямую, перпендику­лярную противоположной стороне (точнее, перпендикулярно пря­мой, содержащей противоположную сторону).

Отрезок этой прямой между вершиной и стороной треугольника или ее продолжением называется высотой тре­угольника.

Конец высоты, отличный от вершины, называется основанием высоты.

Обратите внимание, что для тупоугольного треугольника основание высоты, опущенной из вершины его острого угла, лежит на продолжении его противоположной стороны! Понятно, что у каждого треугольника имеются три медианы, три биссектрисы и три высоты.

Любая прямая, проходящая через центр окружности, является ее осью симметрии.

По определению окружность состоит из всех точек плоскости, удаленных на одно и то же расстояние от ее центра. Проведем через центр окружности точку О — произвольную прямую a.

Пусть А — некоторая точка окружности. Если А лежит на прямой а, то в результате симметрии относительно а точка А останется на месте.

Если же А не принадлежит прямой а, то в результате симметрии она перейдет в некоторую точку А', а отрезок ОА — в отрезок OA'. Согласно свойству симметрии
OA = OA',
а значит, и точка А' принадлежит окружности. Но при этой симметрии точка A', в свою очередь, перейдет в А. Короче говоря, при симметрии относительно прямой a точки А и А', лежащие на окружности, просто поменяются местами. Из этого следует, что вся окружность перейдет сама в себя.

Окружность — это замкнутая плоская кривая, состоящая из всех точек плоскости, удаленных от данной точки O на данное расстояние.

При этом точка O называется центром окружности.

Расстояние от О до точки окружности называется ее радиусом. Заметим, что радиусом называется и сам этот отрезок, и его длина.

Отрезок, соединяющий две точки окружности, называется хордой. Вообще, отрезок, соединяющий две точки любой кривой, является хордой этой кривой.

Хорда, проходящая через центр окружности, есть диаметр окружности.

Фигура, ограниченная окружностью, называется кругом. Окружность и круг обладают многими поистине замечательными свойствами. В некотором смысле это самые симметричные линия и фигура. У окружности и круга есть центр и бесконечно много осей симметрии.

Окружность — это замкнутая плоская кривая, состоящая из всех то­чек плоскости, удаленных от данной точки O на данное расстояние.

Наше определение как бы подтверждает, что кривая, изображаемая с помощью циркуля, в самом деле является окружностью.

Любая замкнутая кривая, не пересекающаяся сама с собой, ограничивает плоскую фигуру и делит плоскость на две части — внутреннюю и внешнюю по отношению к этой фигуре.

При этом, если точка А принадлежит внутренней области, а точка В — внешней, то, двигаясь из А в В по любой кривой, мы пересечем данную замкнутую кривую нечетное число раз.

Это понятно, ведь при каждом пересечении мы переходим из внутренней области во внешнюю или обратно, и сами эти переходы чередуются. При одном пересечении мы перешли из внутренней во внешнюю область, после двух — вернулись обратно, после трех — вновь попадаем во внешнюю область и т.д.

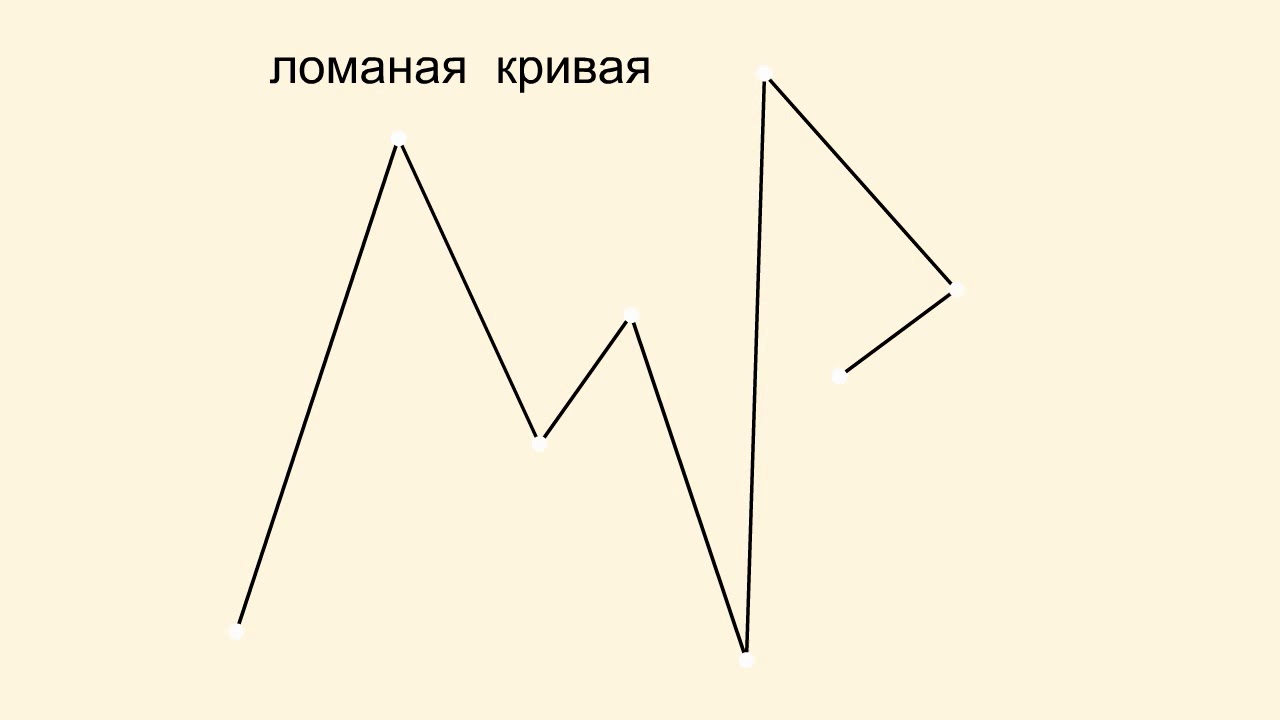
Кривая, состоящая из конечного числа отрезков прямых линий, называется ломаной.

Концы отрезков — вершины ломаной.

Отрезки — звенья, или стороны, ломаной. Соседние стороны не должны лежать на одной прямой.