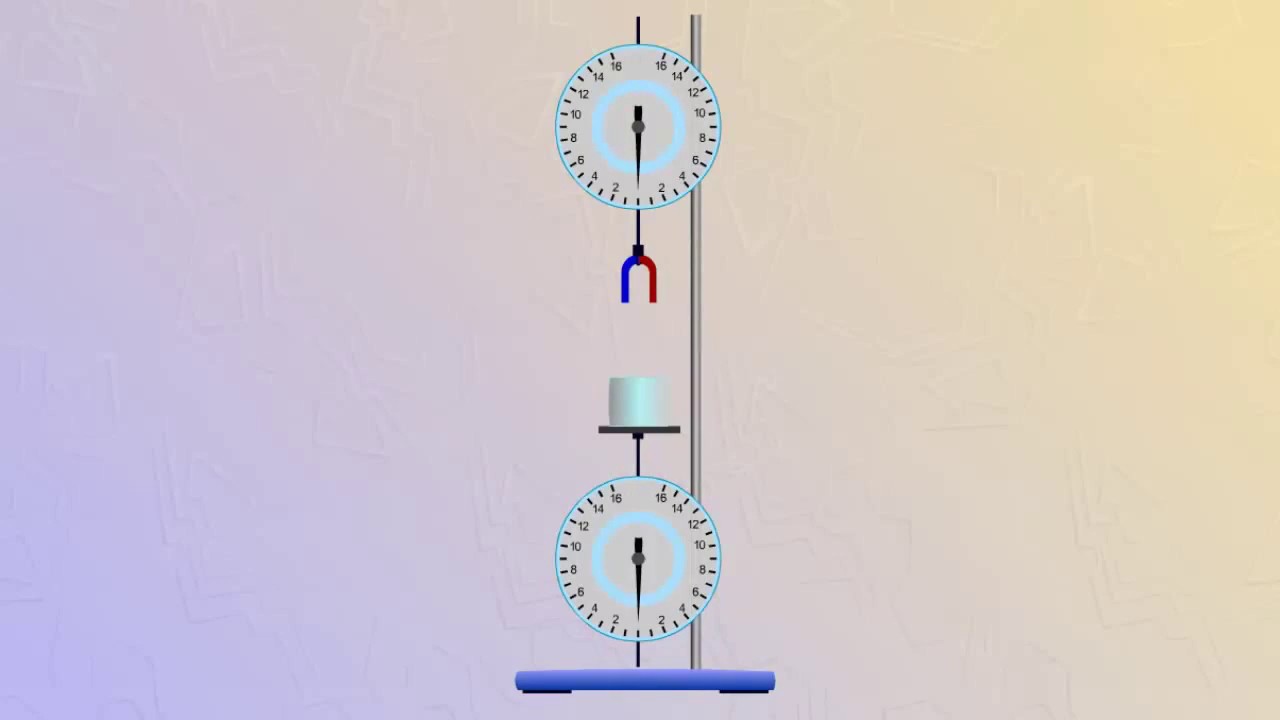
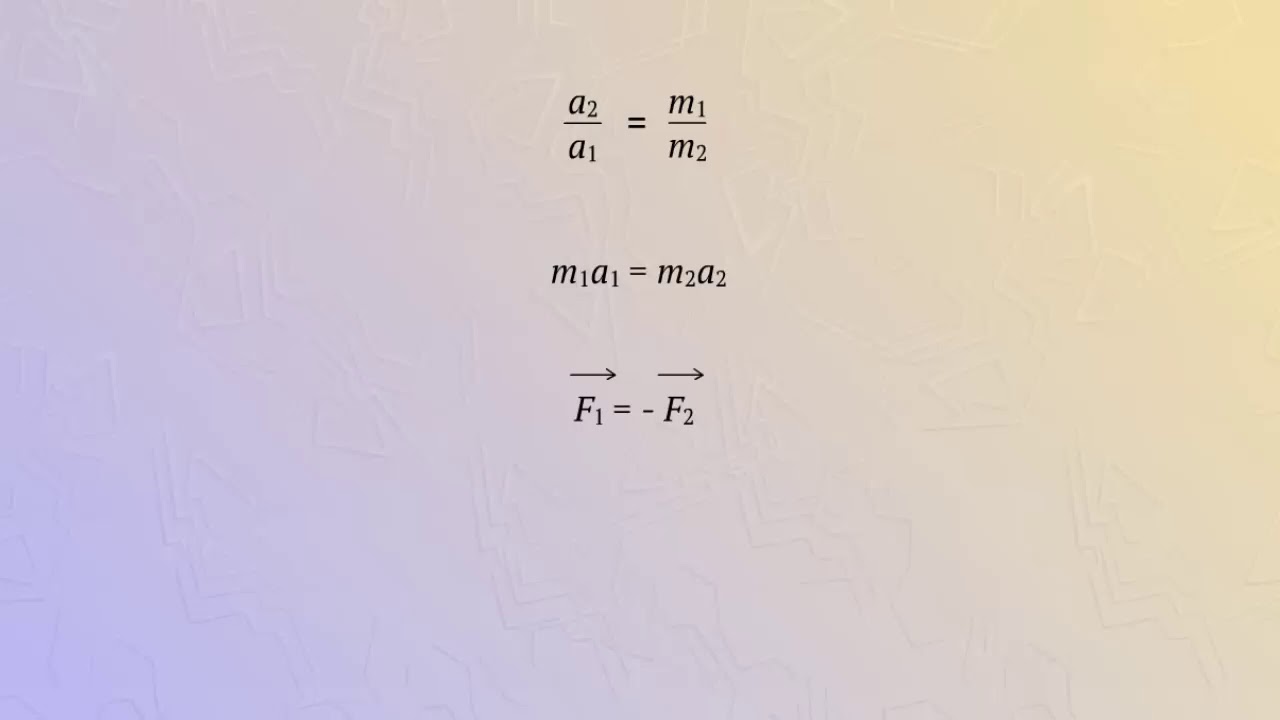Третий признак равенства треугольников

Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Пусть для треугольников ABC и А1В1С1 имеют место равенства:
АВ равно А1В1,
ВС равно В1С1,
СА равно C1A1.

Рассмотрим две окружности с центрами в A и B и радиусами со­ответственно AC и BC. Эти окружности пересекаются в двух симмет­ричных относительно AB точках: C и С2.

Перене­сем треугольник А1В1С1 так, чтобы сторона А1В1 совпала со сторо­ной АВ, при этом должны совпасть вершины А1 и A, В1 и B.

Точка С1 после пе­реноса указанным образом треугольника А1В1С1 должна совпасть либо с точкой C, либо с точкой С2. В обоих случаях это будет означать равенство треугольников ABC и А1В1С1, поскольку треугольни­ки ABC и ABС2 равны, так как эти треугольники симметричны относитель­но прямой AB.