Последние
Прямая, хотя это и звучит немного странно, является частным случаем кривой, причем кривой, бесконечной в обе стороны.
А отрезок прямой — пример конечной кривой. И прямая, и отрезок — незамкнутые и несамопересекающиеся кривые.
Окружность — это пример конечной, замкнутой, несамопересекающейся кривой.
Кривая может быть: конечной и бесконечной, замкнутой и незамкнутой, самопересекающейся и несамопересекающейся.
Все эти названия говорят сами за себя, и вы легко сможете определить, к какому виду относится та или иная кривая.
Плоскую линию, которую можно изобразить на листе бумаги, не отрывая карандаша от листа, будем называть плоской кривой или просто кривой.
На поверхности шара тоже можно нарисовать кривую, но плоской она уже не будет.
Луч с началом в вершине данного угла, лежащий внутри этого угла и делящий его на два равных угла, называется биссектрисой этого угла.
Из определения биссектрисы следует, что прямая, на которой лежит биссектриса, является осью симметрии угла.
Теорема о единственности перпендикуляра подсказывает также и способ построения прямой, перпендикулярной данной, проходящей через точку, расположенную вне данной прямой.
Если точка А расположена вне прямой а, то построим сначала точку А', симметричную А относительно а.
Проведя прямую АА', мы построим нужный перпендикуляр к а, проходящий через точку А.
Через любую точку плоскости проходит единственная прямая, перпендикулярная данной прямой.
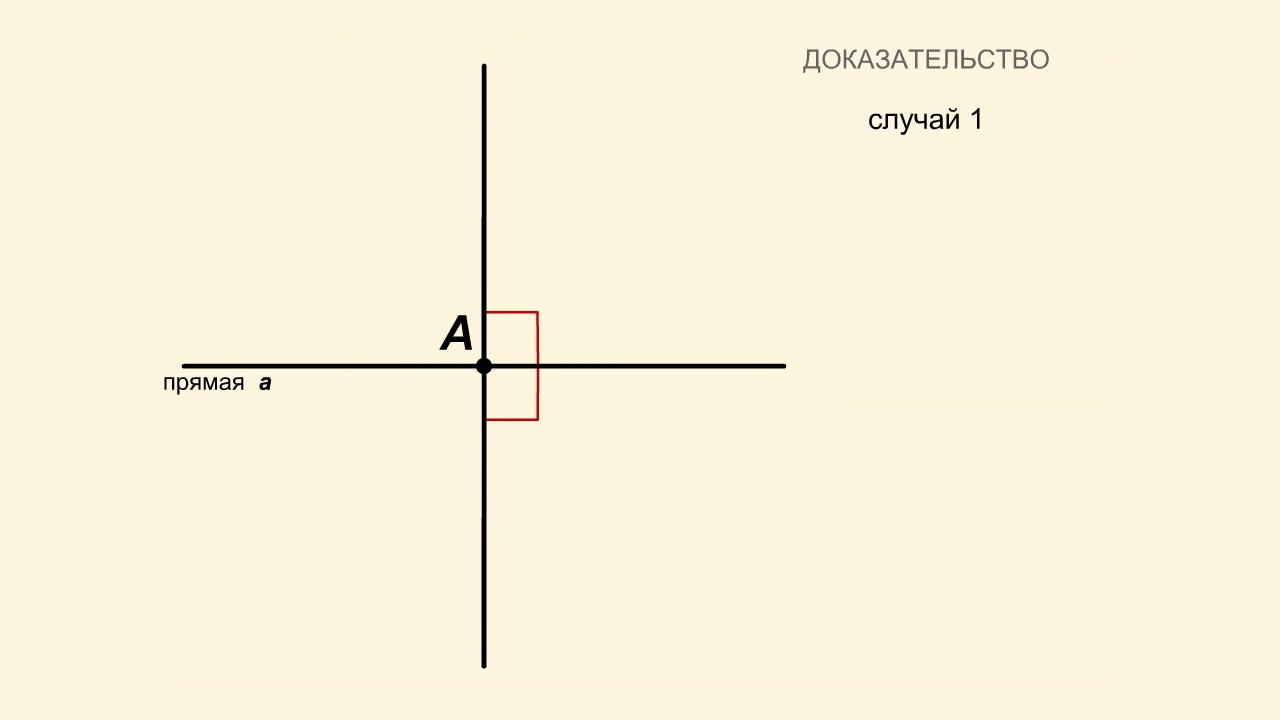
Пусть точка А лежит на прямой а.
В каждой из двух полуплоскостей, соответствующих прямой а, существует лишь один луч, образующий прямые углы с обеими полупрямыми, на которые точка А разбивает прямую а. Эти два луча лежат на одной прямой, перпендикулярной прямой а.
Рассмотрим теперь случай, когда точка А расположена вне прямой.
Обозначим через А' точку, симметричную А относительно а. Как мы уже знаем из теоремы о симметрии перпендикулярных прямых, прямая, перпендикулярная а, в результате симметрии относительно а переходит сама в себя. Это означает, что если она проходила через А, то должна проходить и через А'. Следовательно, эта прямая является единственной.
Если две прямые, лежащие в плоскости, перпендикулярны, то при симметрии относительно одной из них вторая прямая переходит сама в себя.
Если две прямые, лежащие в плоскости, перпендикулярны, то при симметрии относительно одной из них вторая прямая переходит сама в себя.
Из определения симметрии следует, что любая фигура при симметрии переходит в равную ей фигуру. Значит, и угол переходит в равный угол. Обозначим рассматриваемые прямые через a и b. Рассмотрим любой из углов, образованных при их пересечении. Сторонами этого угла являются лучи прямых а1 и b1. Этот угол по условию равен 90°.
В результате симметрии относительно a этот угол перейдет в равный ему угол. Но при этом сторона, лежащая на прямой a (луч a1), останется на месте. Значит, другая сторона (луч b1) перейдет в свое продолжение — другой луч той же прямой b (луч b2).
Величина угла между двумя прямыми равна величине наименьшего из образовавшихся при их пересечении углов.
Из четырех углов, образовавшихся при пересечении двух прямых, хотя бы одна пара вертикальных углов не превосходит 90°.
Величину каждого из таких углов мы и примем за величину угла между прямыми. Иными словами, величина угла между двумя прямыми равна величине наименьшего из образовавшихся при их пересечении углов.
Вертикальные углы равны. Докажем, например, что на рисунке равны углы 1 и 3.
Эти углы являются смежными для угла 2. Каждый из них дополняет до 180° угол 2, а это значит, что углы 1 и 3 равны.
При пересечении двух прямых плоскость делится на четыре части, четыре угла.
Эти четыре угла можно разбить на две пары. В каждую пару будут входить углы, не имеющие общей стороны. Такую пару углов мы будем называть вертикальными.
Если угол равен углу, смежному с ним, то такой угол называется прямым. Величина прямого угла равна 90°.
Углы, меньшие 90°, называются острыми.
Углы от 90° до 180° — тупыми.
Два угла называются смежными, если одна сторона у них общая, а две другие стороны являются дополнительными лучами.
Из определения градусной меры следует, что сумма величин градусных мер смежных углов равна 180°.
Наиболее распространенной мерой углов является градусная мера. С этой мерой вы уже знакомы, поэтому лишь коротко напомним о ней. Величина развернутого угла равна 180 градусам.
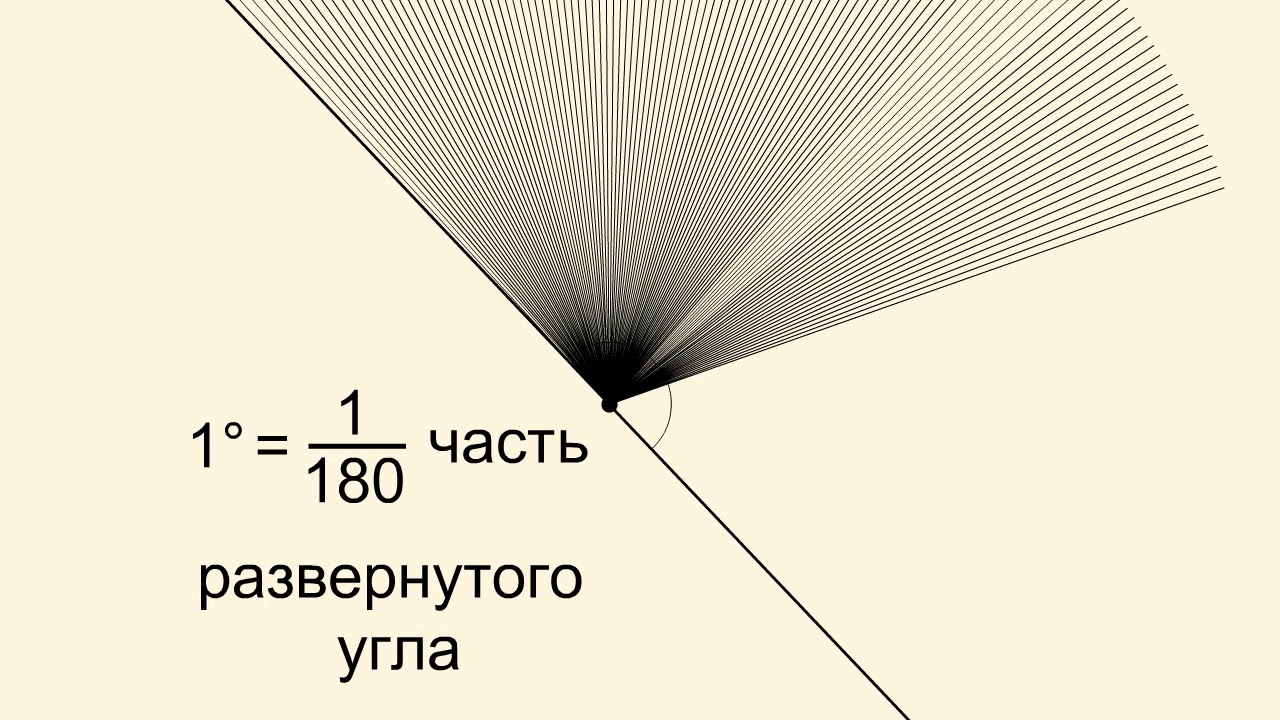
Угол в 1 градус (обозначается 1°) есть 1/180 развернутого угла. Это означает, что если мы приложим друг к другу, как на рисунке, 180 углов по 1° каждый, то в результате получим развернутый угол.
Рассмотрим какой-нибудь угол. Пусть одна его сторона неподвижна, а другая вращается вокруг вершины. Будем считать, что в начальном положении стороны угла совпадают, что соответствует углу 0°, а в конечном положении стороны образуют развернутый угол, величина которого равна 180°. Тогда любой угол, величина которого равна заданному числу градусов, при этом вращении появится лишь однажды.
Развернутый угол – 180°.
Угол, стороны которого лежат на одной прямой и являются дополнительными лучами этой прямой, будем называть развернутым.
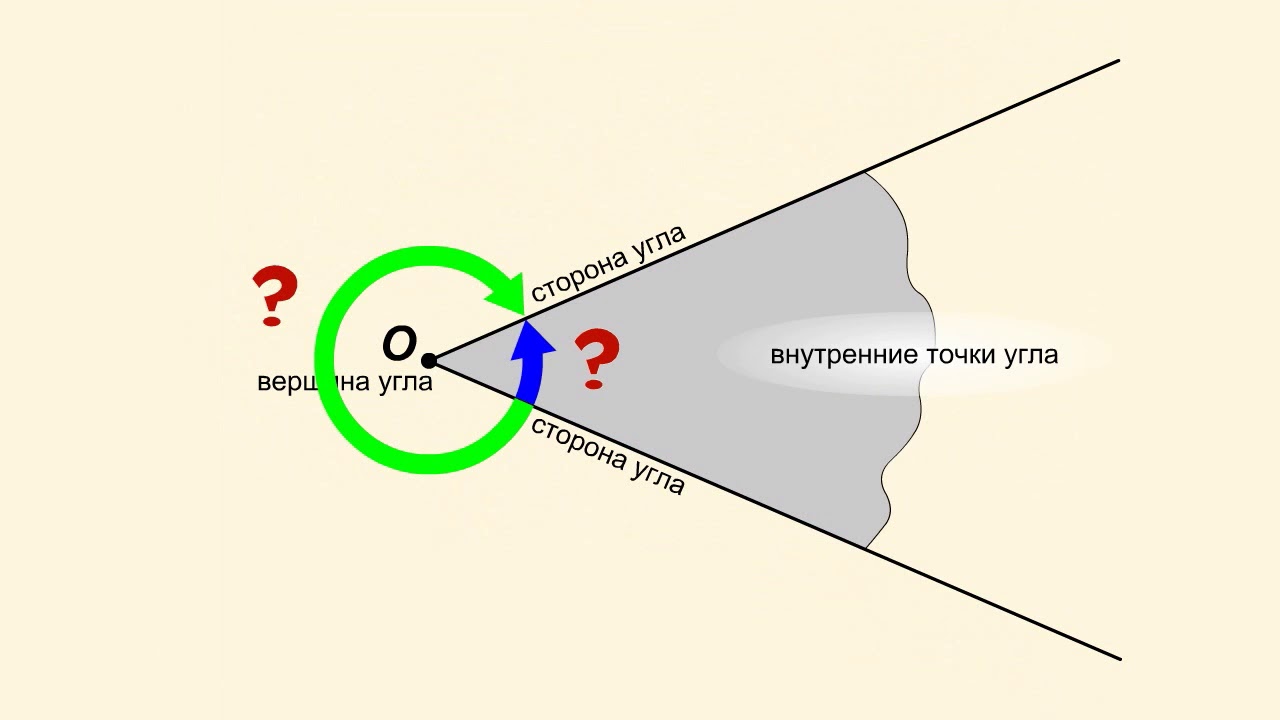
Углом мы будем называть часть плоскости, заключенную между двумя лучами этой плоскости, имеющими общее начало. Точки, лежащие в этой части плоскости, будем называть внутренними точками угла.
Углом мы будем называть часть плоскости, заключенную между двумя лучами этой плоскости, имеющими общее начало. Точки, лежащие в этой части плоскости, будем называть внутренними точками угла.
Лучи, образующие угол, называются сторонами угла, а их общее начало — вершиной угла.
Данное определение угла не указывает, какую из двух частей плоскости, образовавшихся при проведении на плоскости двух лучей с общим началом, следует отнести к самому углу, а какую нет. Договоримся, что обычно мы будем относить к углу меньшую из двух образовавшихся частей. Из этого правила, однако, в некоторых случаях будем делать исключения.
Любая прямая плоскости является осью симметрии плоскости.
Как мы знаем, прямая — это линия пересечения двух плоскостей. Отсюда следует, что при перегибании листа бумаги, представляющего собой модель плоскости, образуется прямая линия. Это станет яснее, если немного развести части листа, получившиеся при его перегибании. Тогда мы увидим, что линия сгиба — это линия пересечения двух плоскостей.
Если точки А и А' совпадут в результате перегибания листа бумаги, то будем говорить, что А и А' симметричны относительно образующейся при перегибании листа прямой а или что они переходят друг в друга при симметрии относительно а. Все точки самой прямой а при этом остаются неподвижными, переходят сами в себя.
Две фигуры или линии плоскости являются симметричными относительно прямой а, если для каждой точки одной фигуры найдется симметричная относительно а точка другой фигуры. Понятно, что симметричные фигуры равны.
Любая прямая плоскости делит эту плоскость на две части — две полуплоскости.
сть в плоскости проведена некоторая прямая, которую мы обозначим буквой а. Любая точка А, не лежащая на этой прямой, находится в одной из двух образовавшихся полуплоскостей.
Если точки А и В расположены в разных полуплоскостях, то отрезок АВ пересекает а.
Если же точки А и B находятся в одной полуплоскости, то отрезок АВ не пересекает а.
Это же можно выразить несколько иначе. Две точки плоскости A и B, не лежащие на прямой в этой плоскости, располагаются в разных или в одной полуплоскости относительно прямой а в зависимости от того, будет отрезок AВ пересекаться с прямой а или нет.
Предположим, что число общих точек у двух прямых более одной.
Согласно первому свойству прямые должны совпасть. А это противоречит условию, что данные прямые различны.
Через любые две точки плоскости можно провести прямую линию и притом только одну.
Прямую, проходящую через точки А и В, мы будем называть прямой АВ.
Как видите, такая прямая — единственная.
Обозначение АВ используется в трех случаях:
— оно может обозначать отрезок или его длину;
— луч;
— прямую.
Но никакой путаницы в наши рассуждения это не внесет, просто в каждом случае будем указывать, о чем идет речь.
Расстояние на плоскости между двумя точками А и В равно длине отрезка АВ. Кратчайший путь из A в B — это путь по прямой, соединяющей эти точки.
Отношение длин любых двух отрезков не зависит от выбора единицы длины. Поэтому мы можем говорить об отношении двух отрезков. Например, если отношение двух отрезков равно двум, то это означает, что в первом отрезке укладывается ровно два отрезка, равных второму отрезку.