Последние
Пример из раздела "Преобразование рациональный выражений"
Презентации по математике (UA):
https://teachua.com/add/matematyka
#решение #пример #математика
Обозначим через В — точку касания касательной с окружностью. Как мы знаем, угол АВО прямой. В прямоугольном треугольнике АВО известен катет ВО, равный радиусу окружности, и гипотенуза АО. По этим данным можно построить треугольник, равный треугольнику АВО.
Для этого построим две перпендикулярные прямые в любом месте плоскости. На одной из прямых от точки Р — точки их пересечения — отложим отрезок РК, равный радиусу окружности.
Проведем окружность радиуса АО с центром в точке К.
Обозначим через М точку пересечения этой окружности со второй прямой.
Получившийся прямоугольный треугольник МРК равен треугольнику АВО по специальному признаку равенства прямоугольных треугольников.
Катет МР равен касательной АВ.
Теперь строим окружность с центром в точке А и радиусом, равным МР.
Точки ее пересечения с данной окружностью будут точками касания.
Соединяя их с А, получим искомые прямые.
Из наших рассуждений следует, что через произвольную точку, расположенную вне окружности, можно провести ровно две прямые, касающиеся этой окружности. При этом отрезки касательных от данной точки до точек касания равны.
Последнее коротко можно выразить следующим образом: касательные к окружности, проведенные из одной точки, равны.
Пример из раздела "Преобразование рациональный выражений"
Презентации по математике (UA):
https://teachua.com/add/matematyka
Пример из раздела "Преобразование рациональный выражений"
Решение по математике 9 класс
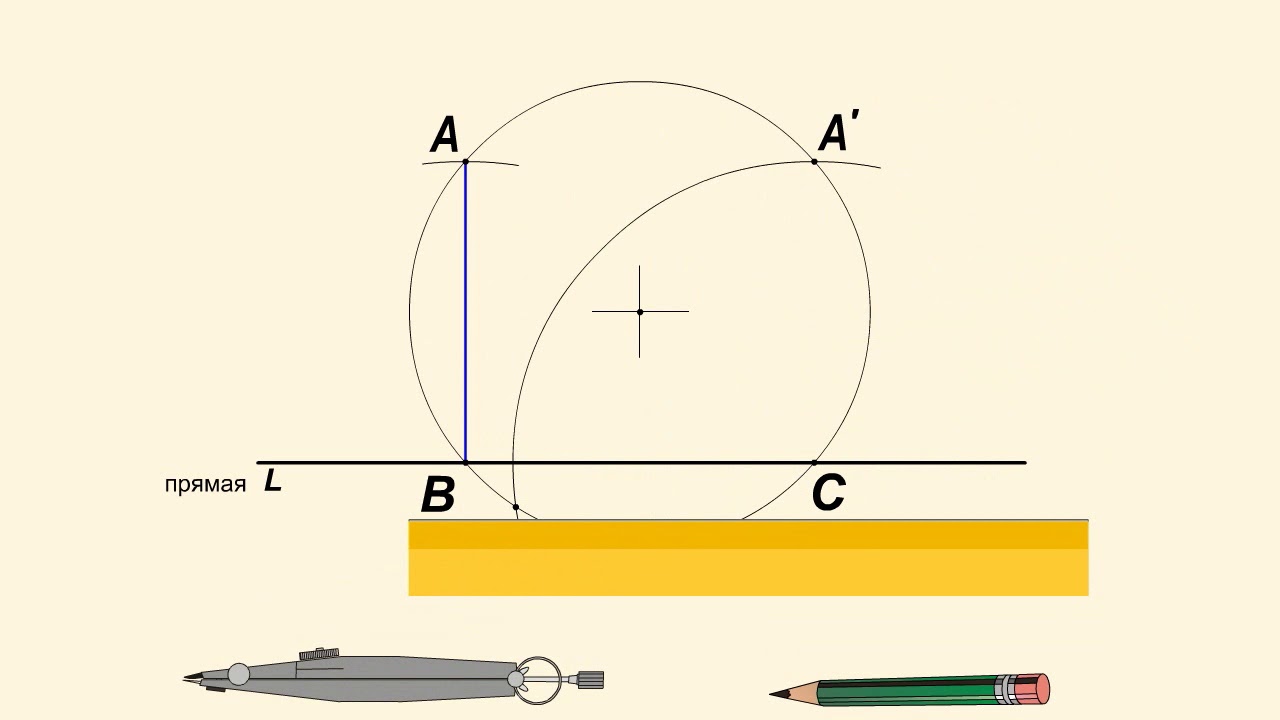
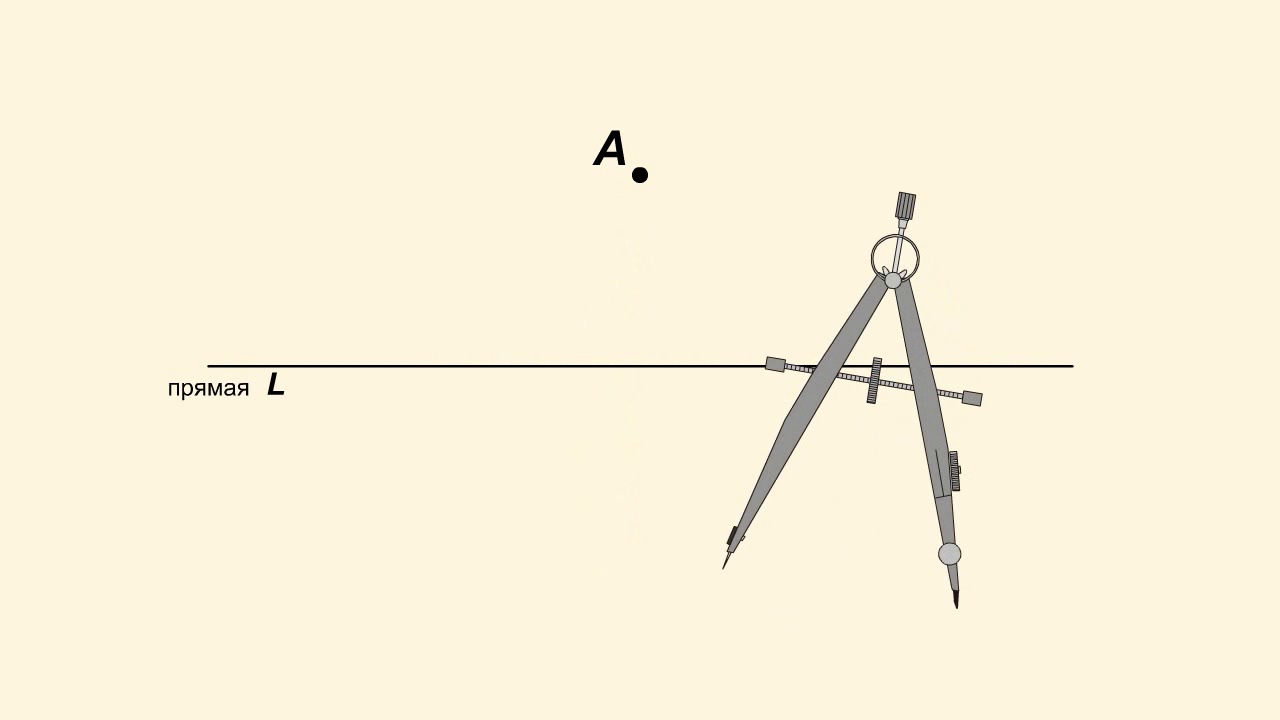
Построим окружность, проходящую через точку А и пересекающую прямую L в точках В и С так, что отрезки АВ и АС не равны.
Для этого центр окружности не должен лежать на перпендикуляре к прямой L, проходящем через А.
Построим теперь еще одну окружность с центром в С и радиусом, равным АВ.
Среди точек пересечения построенных окружностей есть одна точка, соединив которую с А мы получим прямую, параллельную L.
Докажем это.
Рассмотрим прямую P, проходящую через центр первой из построенных окружностей и перпендикулярную L.
При симметрии относительно прямой P точки В и С переходят одна в другую. Точка А перейдет в такую точку А' первой окружности, для которой СА'=ВА.
Это означает, что А' — одна из точек пересечения наших окружностей.
Заметим, что А' не может совпасть с А. Вот для чего потребовалось условие АВ не равно АС.
Прямые L и АА' перпендикулярны одной прямой P, а значит, они параллельны.
Пример из раздела "Преобразование рациональный выражений"
Решение по математике 9 класс
Презентации по математике (UA):
https://teachua.com/add/matematyka
Рассмотрим угол с вершиной А.
Проведем окружность произвольного радиуса с центром в точке А.
Обозначим через В и С точки пересечения окружности со сторонами угла.
Теперь построим две пересекающиеся окружности равного радиуса с центрами в точках В и С.
Возьмем точку их пересечения, лежащую внутри угла. Обозначим ее буквой D.
Треугольники АВD и АСD равны по трем сторонам. Значит, равны углы ВАD и САD.
Луч АD является биссектрисой рассматриваемого угла.
2 Преобразование рациональных выражений
Упростить - значит представить рациональное выражение в виде дроби, у которой числитель и знаменатель есть целые выражения.
Необходимо уметь:
• Сокращать дробь
• Приводить дроби к общему знаменателю
• Складывать и вычитать рациональные дроби
• Умножать и делить дроби
• Применять различные способы разложения многочлена на множители
• Возводить дробь в целую степень.
Пример из раздела "Разложение многочленов на множители"
Решение по математике 9 класс
Презентации по математике (UA):
https://teachua.com/add/matematyka
Это построение легко сводится к построению треугольника, равного данному.
Выберем на сторонах угла произвольно по точке. Пусть это точки В и С.
Откладываем в нужном месте отрезок, равный AB.
Затем с центрами в концах этого отрезка строим две окружности, радиусы которых равны AC и BC.
Находим точку пересечения построенных окружностей.
Пример из раздела "Разложение многочленов на множители"
Решение задания по математике
Презентации по математике (UA):
https://teachua.com/add/matematyka
1 Разложение многочлена на множители
Математика 9 класс
Методы разложения на множители
1) Вынесение за скобки общего множителя
2) Применение тождеств сокращенного умножения
3) Группировка
Статья про разложение многочленов на множители:
https://fizmat.teachua.com/?p=81
Если на плоскости изображен треугольник, то мы без труда сможем в любом месте плоскости построить треугольник, равный изображенному.
Будем исходить из третьего признака равенства треугольников.
Откладываем в нужном месте отрезок, равный одной из сторон треугольника.
Затем с центрами в концах этого отрезка строим две окружности, радиусы которых равны двум другим сторонам.
Находим точку пересечения построенных окружностей.
Точно так же строится треугольник по трем сторонам. Разница лишь в том, что дано не изображение треугольника, а три отрезка, равные его сторонам.
Задача сводится к построению серединного перпендикуляра к АВ.
Точка его пересечения с АВ является искомой.
Построим две одинаковые пересекающиеся окружности с центрами А и В.
Проведем прямую через точки их пересечения и найдем точку пересечения этой прямой с АВ.
Это и есть искомая середина отрезка АВ.
Для построения перпендикуляра достаточно сначала построить точку А', симметричную А относительно L.
Для этого построим две окружности с центрами на L, проходящие через точку А. Вторая точка пересечения этих окружностей и даст точку А'.
Проведя прямую АА', мы получим искомый перпендикуляр.
Прежде чем перейти к рассмотрению конкретных задач, напомним о тех условностях, которые связаны с задачами на построение.
Во всех таких задачах, если не сделано оговорок, речь идет о построении с помощью циркуля и линейки.
С помощью линейки мы можем через любые две точки плоскости провести прямую линию. И ничего более! Математическая линейка односторонняя и не имеет делений.
С помощью циркуля мы можем построить окружность с заданным центром и заданным радиусом. При этом радиус задается указанием таких двух точек на плоскости, расстояние между которыми равно радиусу.
С помощью циркуля мы можем также отложить отрезок, равный данному.
Биссектрису угла также можно рассматривать как геометрическое место точек.
Докажем, что геометрическим местом точек, расположенных внутри данного угла и равноудаленных от его сторон, является биссектриса этого угла.
Проведем следующие рассуждения.
Первое рассуждение.
Если точка М расположена внутри угла и находится на равных расстояниях от его сторон, то М лежит на биссектрисе этого угла.
Доказательство.
Опустив перпендикуляры МА и МВ на стороны угла, из равенства МА = МВ на основании соответствующего признака равенства прямоугольных треугольников получим, что треугольники ОМА и ОМВ равны. Значит, равны углы МОА и МОВ, т.е. OM — биссектриса угла АОВ.
Второе рассуждение.
Если точка М лежит на биссектрисе, то М равноудалена от сторон угла.
Доказательство.
При симметрии относительно прямой, содержащей биссектрису, стороны угла перейдут друг в друга.
Напомним, что через любую точку плоскости проходит единственный перпендикуляр к заданной прямой.
Что представляет собой геометрическое место точек плоскости, равноудаленных от концов заданного отрезка прямой на плоскости?
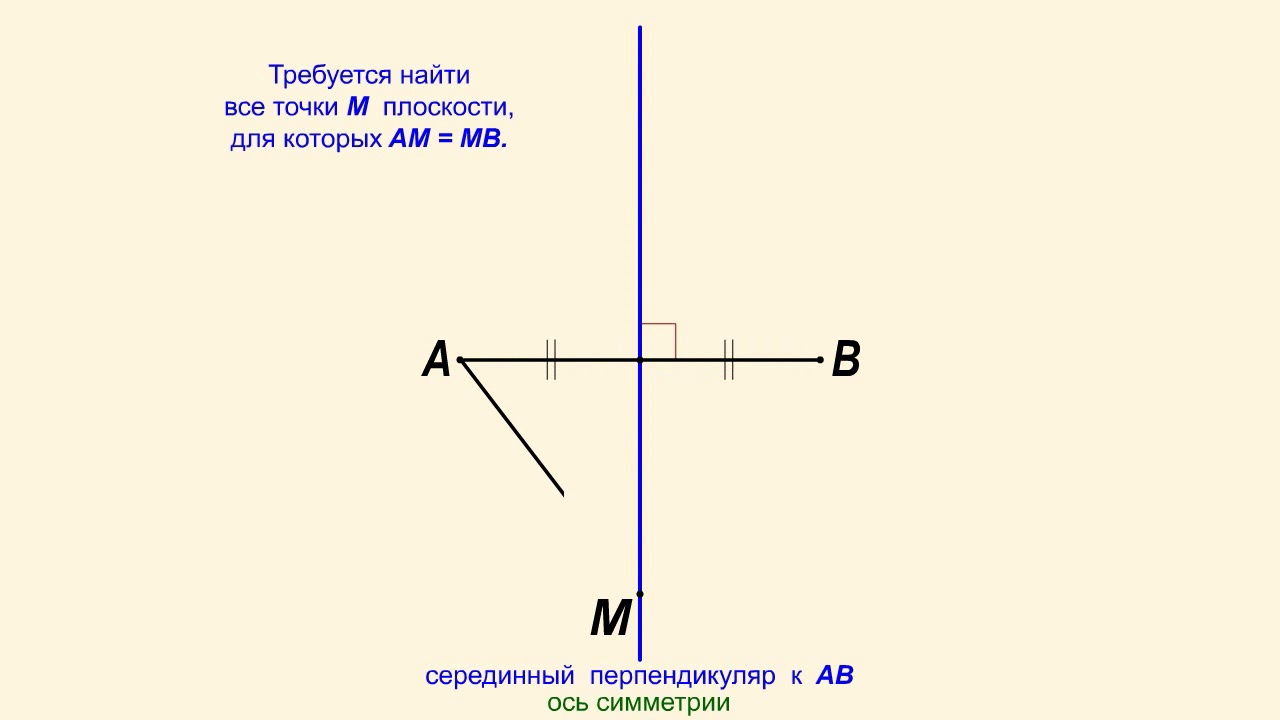
Дан отрезок АВ, который лежит в некоторой плоскости. Требуется найти все точки M плоскости, для которых AM = MB.
Ответ следует из известных вам свойств равнобедренного треугольника.
Искомым геометрическим местом точек является прямая, перпендикулярная АВ и проходящая через середину АВ. Такую прямую называют серединным перпендикуляром к АВ.
Серединный перпендикуляр является осью симметрии, при которой А переходит в В, и наоборот.
В самом деле, если М — такая точка плоскости, что АМ = МВ, то согласно свойству равнобедренного треугольника М принадлежит серединному перпендикуляру.
Если же точка М принадлежит серединному перпендикуляру к АВ, то, по теореме о признаках равнобедренного треугольника, треугольник АМВ — равнобедренный и АМ = МВ.
Если мы построим окружность радиуса AB с центром в точке А, то эта окружность будет иметь единственную общую точку с прямой L — точку В.
Если прямая имеет единственную общую точку с окружностью, то такая прямая называется касательной к окружности.
О такой прямой говорят также, что она касается окружности.
Общая точка окружности и касательной называется точкой касания.
В любом треугольнике против большей стороны лежит больший угол. И наоборот, против большего угла лежит большая сторона.
Пусть в треугольнике АВС сторона АС больше стороны АВ.
Возьмем на стороне АС точку D так, что АD = АВ.
В равнобедренном треугольнике АВD, как известно, равны углы AВD и АDВ. Но угол АВD меньше угла АВС, а угол АDВ по теореме о внешнем угле больше угла ВСА. Значит, тем более угол АВС больше угла ВСА.
А теперь от углов — к сторонам. Пусть в треугольнике АВС угол АВС больше угла АСВ. Тогда из только что доказанного следует, что сторона АВ не может быть больше стороны АС. Стороны АВ и АС не могут быть и равными. Остается единственное: АВ меньше АС.