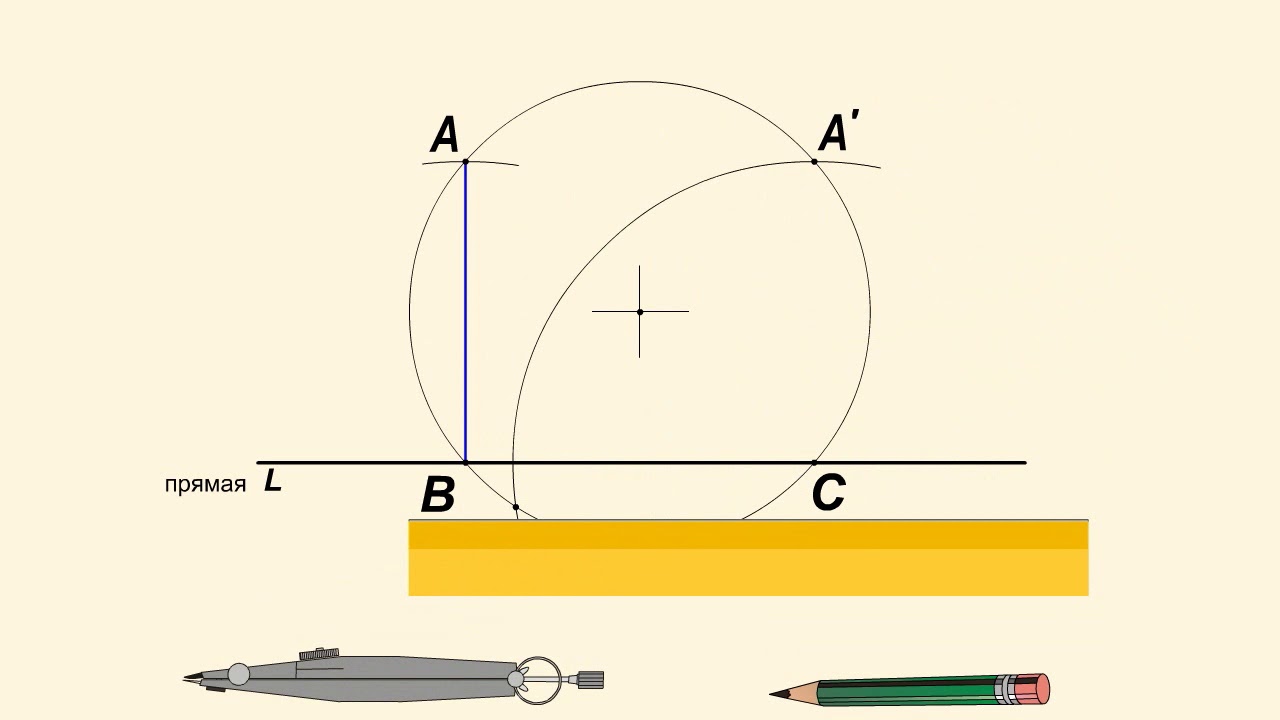
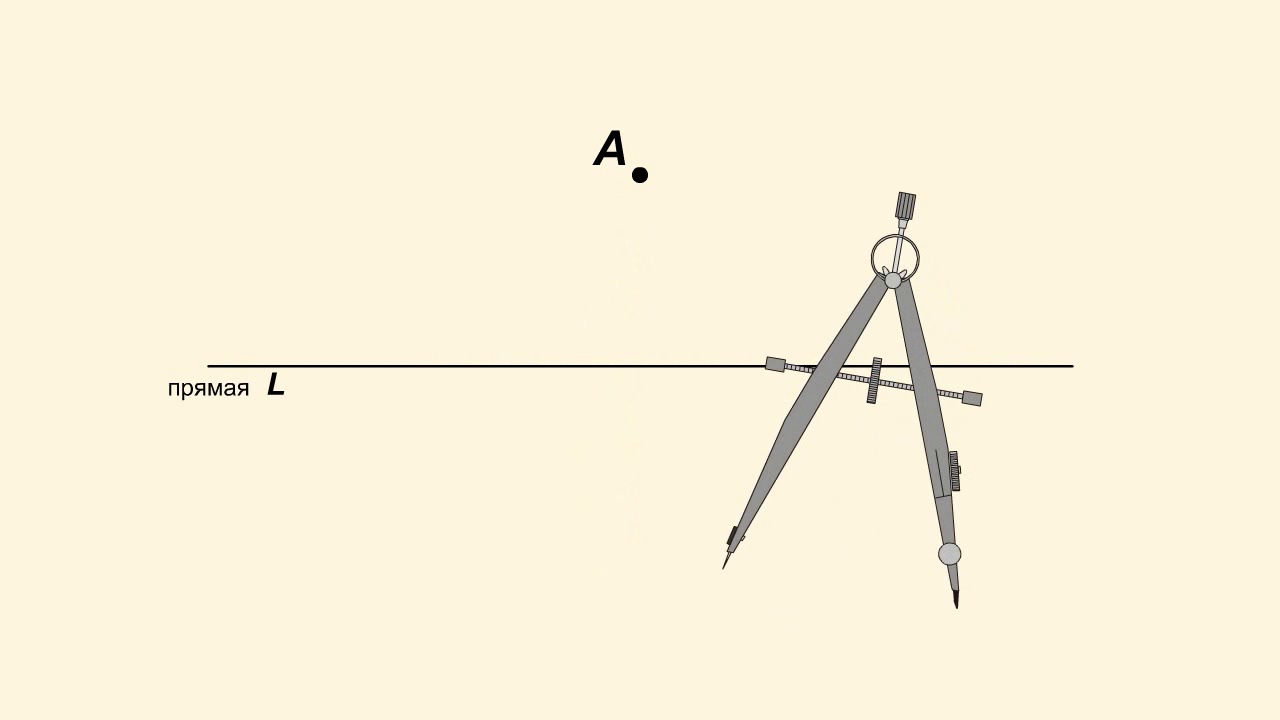
Построение касательной к окружности

Обозначим через В — точку касания касательной с окружностью. Как мы знаем, угол АВО пря­мой. В прямоугольном треугольнике АВО известен катет ВО, равный радиусу окружности, и гипотенуза АО. По этим данным можно по­строить треугольник, равный треугольнику АВО.

Для этого построим две перпендикулярные прямые в любом месте плоскости. На одной из прямых от точки Р — точки их пере­сечения — отложим отрезок РК, равный радиусу окружности.

Прове­дем окружность радиуса АО с центром в точке К.

Обозначим через М точку пересечения этой окружности со второй прямой.

Получившийся прямоугольный треугольник МРК равен тре­угольнику АВО по специальному признаку равенства прямоугольных треугольни­ков.

Катет МР равен касательной АВ.

Теперь строим ок­ружность с центром в точке А и радиусом, равным МР.

Точки ее пе­ресечения с данной окружностью будут точками касания.

Соединяя их с А, получим искомые прямые.

Из наших рассуждений следует, что через произвольную точку, расположенную вне окружности, можно провести ровно две пря­мые, касающиеся этой окружности. При этом отрезки касательных от данной точки до точек касания равны.

Последнее коротко можно выразить следующим образом: касательные к окружности, проведенные из одной точки, равны.