Рассмотрим классическую геометриче­скую задачу такого рода, которой очень легко придать заниматель­ный вид. Но мы этого делать не будем и ограничимся сухой матема­тической формулировкой.

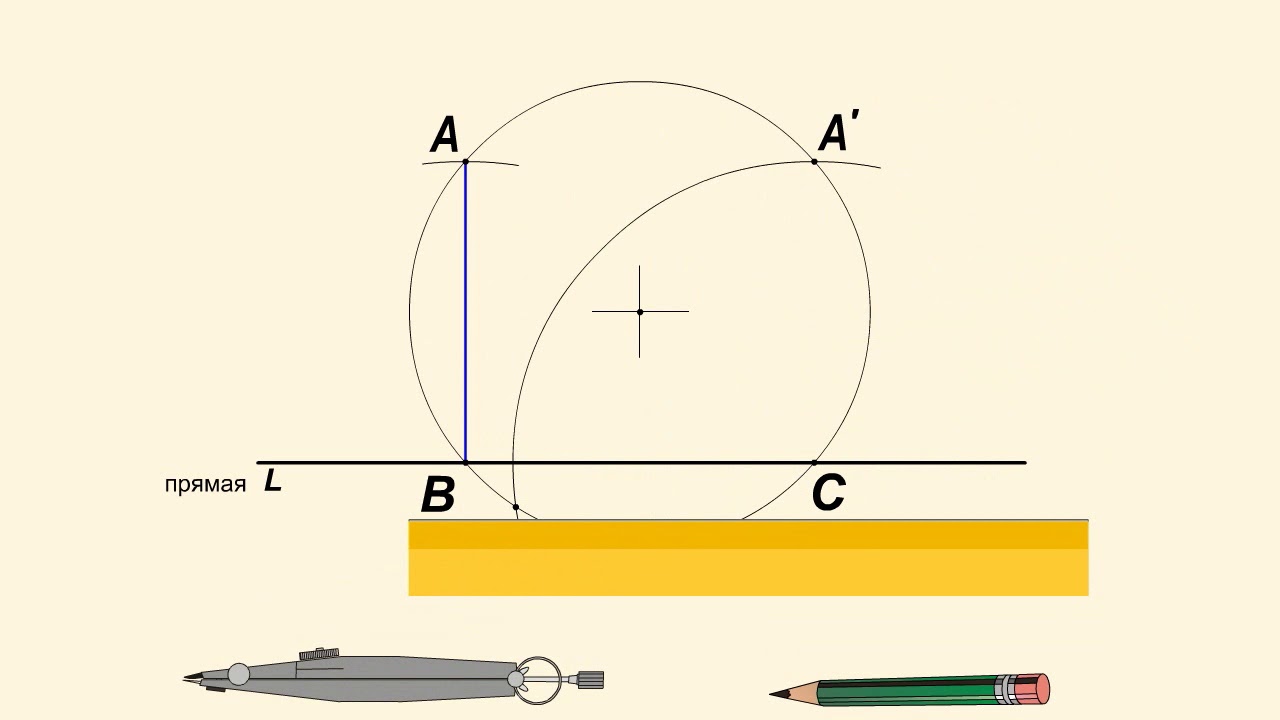
Дана прямая L и две точки А и В по одну сторону от нее. Най­дите на прямой L точку М такую, чтобы длина двузвенной ломаной АМВ была наименьшей.

Решение задачи затрудняет то, что точки А и В расположены по одну сторону от L. Вот если бы... (впрочем, не будем пытаться пока­зать, каким образом смутная догадка может оформиться в настоя­щее решение). Рассмотрим само решение.

Возьмем любую точку М на прямой L. Построим точку А', симметричную А относительно L. Поскольку АМ=А'М, длина ломаной АМВ всегда равна длине ломаной А'МВ.

Но последняя будет наименьшей, когда она превращается в отрезок прямой. Значит, искомой точкой на L будет точка, в которой ее пересечет отрезок А'В. Обозначим ее через М0.

Из соответствующих свойств углов следует, что для найденной точки М0 лучи М0A и М0В образуют с L равные углы.

Именно по та­кому закону происходит отражение света, т.е. если бы мы смогли направить луч света из А так, чтобы он, отразившись от прямой L, попал в В, то этот луч реализовал бы кратчайший путь.

Как мы знаем, чтобы попасть из одной точки плоскости в другую кратчайшим путем, надо двигаться по прямой линии. Это простей­шая задача на отыскание кратчайшего пути.

Существует ряд гораздо более сложных, интересных и важных для практики задач подобного рода. Например, соединить несколько городов дорогами так, чтобы можно было проехать в каждый город из любого другого, а общая дли­на построенных дорог была наименьшей.

Обозначим через В — точку касания касательной с окружностью. Как мы знаем, угол АВО пря­мой. В прямоугольном треугольнике АВО известен катет ВО, равный радиусу окружности, и гипотенуза АО. По этим данным можно по­строить треугольник, равный треугольнику АВО.

Для этого построим две перпендикулярные прямые в любом месте плоскости. На одной из прямых от точки Р — точки их пере­сечения — отложим отрезок РК, равный радиусу окружности.

Прове­дем окружность радиуса АО с центром в точке К.

Обозначим через М точку пересечения этой окружности со второй прямой.

Получившийся прямоугольный треугольник МРК равен тре­угольнику АВО по специальному признаку равенства прямоугольных треугольни­ков.

Катет МР равен касательной АВ.

Теперь строим ок­ружность с центром в точке А и радиусом, равным МР.

Точки ее пе­ресечения с данной окружностью будут точками касания.

Соединяя их с А, получим искомые прямые.

Из наших рассуждений следует, что через произвольную точку, расположенную вне окружности, можно провести ровно две пря­мые, касающиеся этой окружности. При этом отрезки касательных от данной точки до точек касания равны.

Последнее коротко можно выразить следующим образом: касательные к окружности, проведенные из одной точки, равны.

Построим окружность, проходящую через точку А и пе­ресекающую прямую L в точках В и С так, что отрезки АВ и АС не равны.

Для этого центр окружности не должен лежать на пер­пендикуляре к прямой L, проходящем через А.

Построим теперь еще одну окружность с центром в С и радиусом, равным АВ.

Среди точек пересечения построенных окружностей есть одна точка, соединив которую с А мы получим прямую, параллельную L.

Дока­жем это.

Рассмотрим прямую P, проходящую через центр первой из построенных окружностей и перпендикулярную L.

При симметрии относительно прямой P точки В и С переходят одна в другую. Точка А перейдет в такую точку А' первой окружности, для которой СА'=ВА.

Это означает, что А' — одна из точек пе­ресечения наших окружностей.

Заметим, что А' не может совпасть с А. Вот для чего потребовалось условие АВ не равно АС.

Прямые L и АА' перпендикулярны одной прямой P, а значит, они параллельны.

Рассмотрим угол с вершиной А.

Проведем окружность произвольного радиуса с центром в точке А.

Обозначим через В и С точки пересечения окружности со сторонами угла.

Теперь построим две пересекающиеся окружности равного радиуса с цен­трами в точках В и С.

Возьмем точку их пересечения, лежащую внут­ри угла. Обозначим ее буквой D.

Треугольники АВD и АСD равны по трем сторонам. Значит, равны углы ВАD и САD.

Луч АD является биссектрисой рассматриваемого угла.

Это построение легко сводится к построению треуголь­ника, равного данному.

Выберем на сторонах угла произвольно по точке. Пусть это точки В и С.

Откладываем в нужном месте отрезок, равный AB.

Затем с центрами в концах этого отрезка строим две окружности, радиусы которых равны AC и BC.

Находим точку пересечения построенных окружностей.

Если на плоскости изображен треугольник, то мы без труда сможем в любом месте плоскости построить треугольник, равный изобра­женному.

Будем исходить из третьего признака равенства треуголь­ников.

Откладываем в нужном месте отрезок, равный одной из сто­рон треугольника.

Затем с центрами в концах этого отрезка строим две окружности, радиусы которых равны двум другим сторонам.

Находим точку пересечения построенных окружностей.

Точно так же строится треугольник по трем сторонам. Разница лишь в том, что дано не изображение треугольника, а три отрезка, равные его сторонам.

Задача сводится к построению серединного перпендикуляра к АВ.

Точка его пересечения с АВ является искомой.

Построим две одинаковые пересекающиеся окружности с центрами А и В.

Проведем прямую через точки их пере­сечения и найдем точку пересечения этой прямой с АВ.

Это и есть искомая середина отрезка АВ.

Для построения перпендикуляра достаточно сначала по­строить точку А', симметричную А относительно L.

Для этого по­строим две окружности с центрами на L, проходящие через точку А. Вторая точка пересечения этих окружностей и даст точку А'.

Проведя прямую АА', мы получим искомый перпендикуляр.

Прежде чем перейти к рассмотрению конкретных задач, напом­ним о тех условностях, которые связаны с задачами на построение.

Во всех таких задачах, если не сделано оговорок, речь идет о по­строении с помощью циркуля и линейки.

С помощью линейки мы можем через любые две точки плоско­сти провести прямую линию. И ничего более! Математическая ли­нейка односторонняя и не имеет делений.

С помощью циркуля мы можем построить окружность с задан­ным центром и заданным радиусом. При этом радиус задается ука­занием таких двух точек на плоскости, расстояние между которыми равно радиусу.

С помощью циркуля мы можем также отложить отрезок, равный данному.

Биссектрису угла также можно рассматривать как геометрическое место точек.

Докажем, что геометрическим местом точек, располо­женных внутри данного угла и равноудаленных от его сторон, является биссектриса этого угла.

Проведем сле­дующие рассуждения.

Первое рассуждение.

Если точка М расположена внутри угла и находится на равных расстояниях от его сторон, то М лежит на биссектрисе этого угла.

Доказательство.

Опустив перпендикуляры МА и МВ на стороны угла, из равенства МА = МВ на основании соответствующего признака равенства прямоугольных треугольников получим, что треугольни­ки ОМА и ОМВ равны. Значит, равны углы МОА и МОВ, т.е. OM — биссектриса угла АОВ.

Второе рассуждение.

Если точка М лежит на биссектрисе, то М равноудалена от сторон угла.

Доказательство.

При симметрии относи­тельно прямой, содержащей биссектрису, стороны угла перейдут друг в друга.

Напомним, что через любую точку плоскости проходит единствен­ный перпендикуляр к заданной прямой.

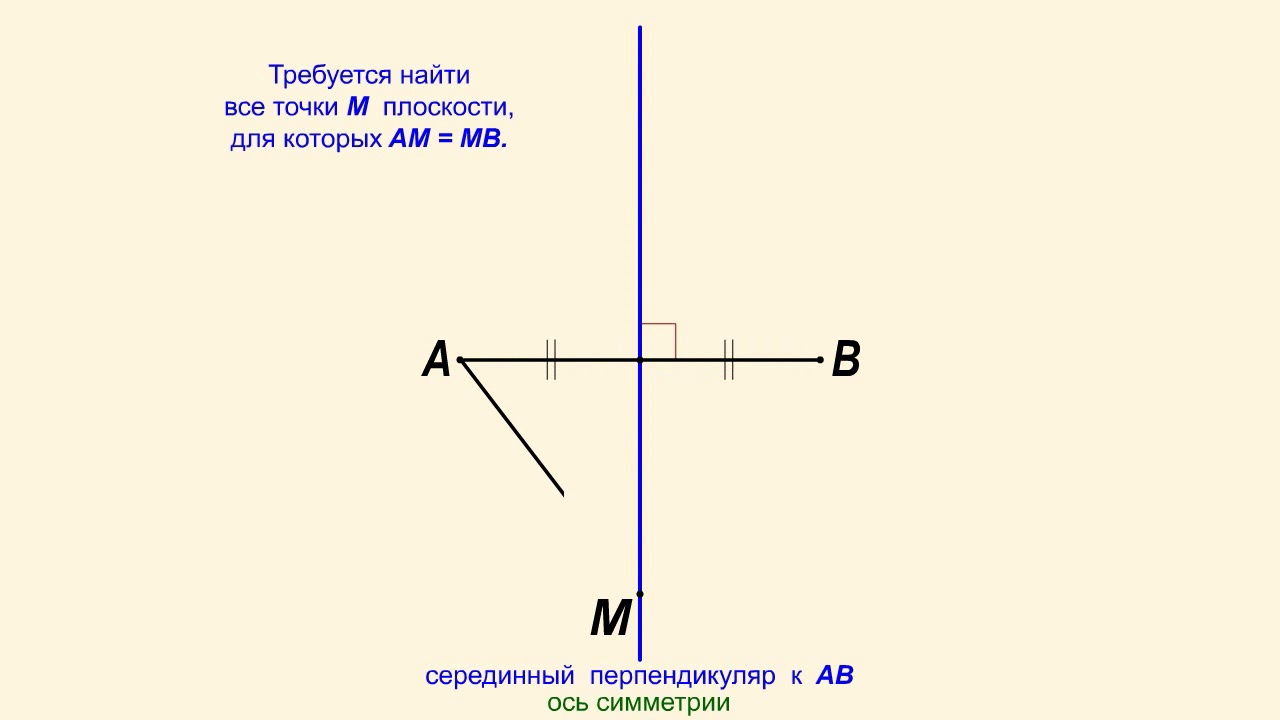
Что представляет собой геометрическое место точек плоскости, равноудаленных от концов заданного отрезка прямой на плоскости?

Дан отрезок АВ, который лежит в некоторой плоскости. Требуется найти все точки M плоскости, для которых AM = MB.

Ответ следует из известных вам свойств равнобедренно­го треугольника.

Искомым геометрическим местом точек является прямая, пер­пендикулярная АВ и проходящая через середину АВ. Та­кую прямую называют серединным перпендикуляром к АВ.

Середин­ный перпендикуляр является осью симметрии, при которой А пере­ходит в В, и наоборот.

В самом деле, если М — такая точка плоскости, что АМ = МВ, то со­гласно свойству равнобедренного треугольника М принадлежит сере­динному перпендикуляру.

Если же точка М принадлежит серединному перпендикуляру к АВ, то, по теореме о признаках равнобедренного треугольника, треугольник АМВ — равнобедренный и АМ = МВ.

Если мы построим окружность радиуса AB с центром в точке А, то эта окружность будет иметь единственную общую точку с прямой L — точку В.

Если прямая имеет единственную общую точку с окружностью, то такая прямая называется касательной к окружности.

О такой прямой говорят также, что она касается окружности.

Общая точка окружности и касательной называется точкой касания.

В любом треугольнике против большей стороны лежит больший угол. И наоборот, против большего угла лежит большая сторона.

Пусть в треугольнике АВС сторона АС больше сто­роны АВ.

Возьмем на стороне АС точку D так, что АD = АВ.

В равнобедренном треугольнике АВD, как известно, равны углы AВD и АDВ. Но угол АВD меньше угла АВС, а угол АDВ по теореме о внешнем угле больше угла ВСА. Значит, тем более угол АВС больше угла ВСА.

А теперь от углов — к сторонам. Пусть в треугольнике АВС угол АВС больше угла АСВ. Тогда из только что доказанного следует, что сторона АВ не может быть больше стороны АС. Стороны АВ и АС не могут быть и равными. Остается единственное: АВ меньше АС.

Внешний угол треугольника больше любого внутреннего, с ним не смежного.

Рассмотрим треугольник АВС и какой-либо из его внешних углов, например угол, смежный с углом АСВ. Докажем, что он больше угла CВA.

Проведем медиану АD и продолжим ее за точку D на такое же рас­стояние. Получим точку A1.

Треугольник DСА1 равен треугольнику DBА (по первому при­знаку), откуда DBА = DСА1. Но угол DСА1 меньше угла, смежного с углом АСВ, поскольку составляет его часть.

Два прямоугольных треугольника равны, если гипотенуза и ка­тет одного треугольника соответственно равны гипотенузе и катету другого.

Кроме того, из первого признака равенства треугольников сле­дует равенство прямоугольных треугольников по двум катетам.

Прямоугольным называется треугольник, у которого есть прямой угол.

Стороны, заключающие прямой угол прямоугольного треугольни­ка, называются катетами прямоугольного треугольника.

Сторона, противоположная прямому углу, называется гипотену­зой прямоугольного треугольника.

Треугольник, как правило, задается тремя элементами.

Пусть в треугольниках ABC и А1В1С1 имеют место равенства АВ = А1В1, AС = A1С1, АВС = А1В1С1.

Обязательно ли такие треугольники равны?

Для того чтобы доказать, что такие треугольники могут быть и неравными, достаточно «предъявить» два неравных треугольника, у которых равны указан­ные в условии элементы. Как говорят математики, построить опро­вергающий пример.

Рассмотрим на плоскости какой-нибудь острый угол, вершину которого обозначим буквой В.

Возьмем на одной из его сторон точку А и с центром в этой точке нарисуем окруж­ность, которая пересекает другую сторону угла в двух точках. Обо­значим эти точки через С и С1.

Один из двух получившихся тре­угольников — это АВС, а другой — АВС1 (можно считать, что точки А и A1, В и В1 совпадают).

Как видим, эти треугольники не равны, хотя и удовлетворяют всем условиям нашей задачи.

Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Пусть для треугольников ABC и А1В1С1 имеют место равенства:
АВ равно А1В1,
ВС равно В1С1,
СА равно C1A1.

Рассмотрим две окружности с центрами в A и B и радиусами со­ответственно AC и BC. Эти окружности пересекаются в двух симмет­ричных относительно AB точках: C и С2.

Перене­сем треугольник А1В1С1 так, чтобы сторона А1В1 совпала со сторо­ной АВ, при этом должны совпасть вершины А1 и A, В1 и B.

Точка С1 после пе­реноса указанным образом треугольника А1В1С1 должна совпасть либо с точкой C, либо с точкой С2. В обоих случаях это будет означать равенство треугольников ABC и А1В1С1, поскольку треугольни­ки ABC и ABС2 равны, так как эти треугольники симметричны относитель­но прямой AB.

Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней уг­лам другого треугольника, то такие треугольники равны.

Пусть в треугольниках АВС и А1В1С1 имеют ме­сто равенства ВС = В1С1, АВС = А1В1С1, а АСВ = А1С1В1.

Наложим тре­угольник А1В1С1 на треугольник АВС так, чтобы совпали стороны ВС и В1С1 и прилегающие к ним углы.

При необходимости треугольник А1В1С1 можно «перевернуть обратной стороной».

Тогда треугольники совпадут полностью. Значит, они равны.