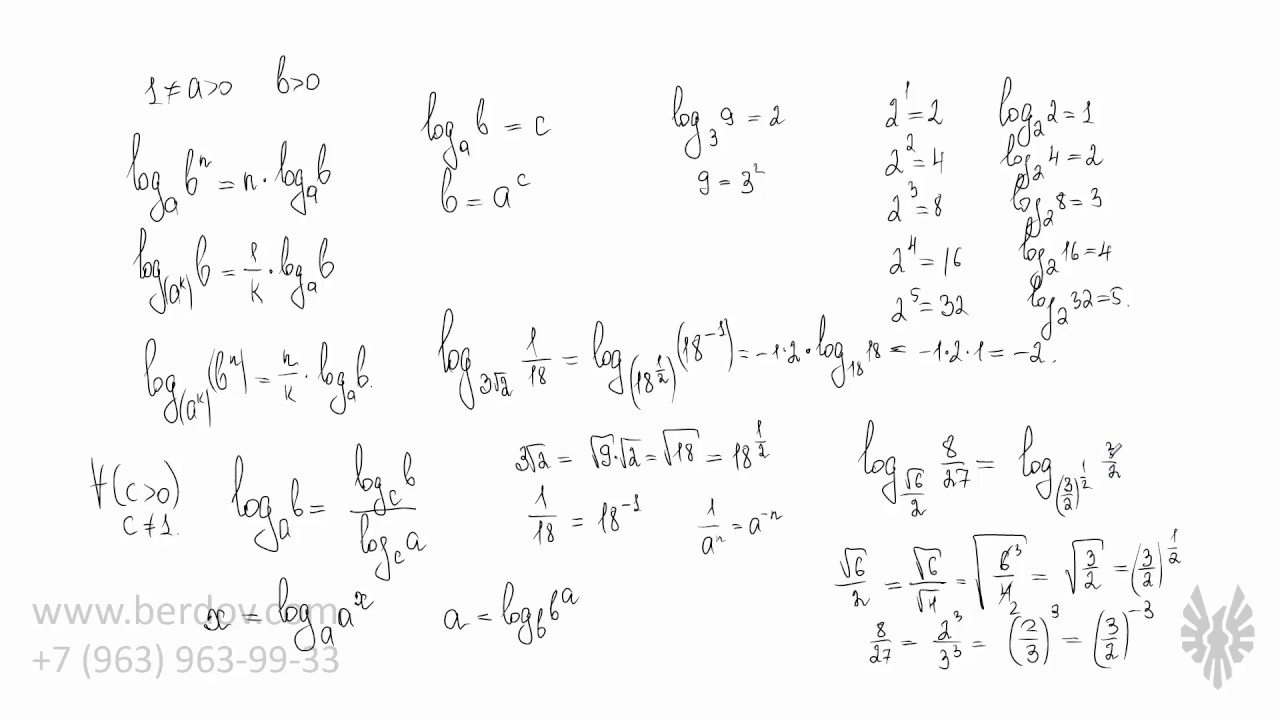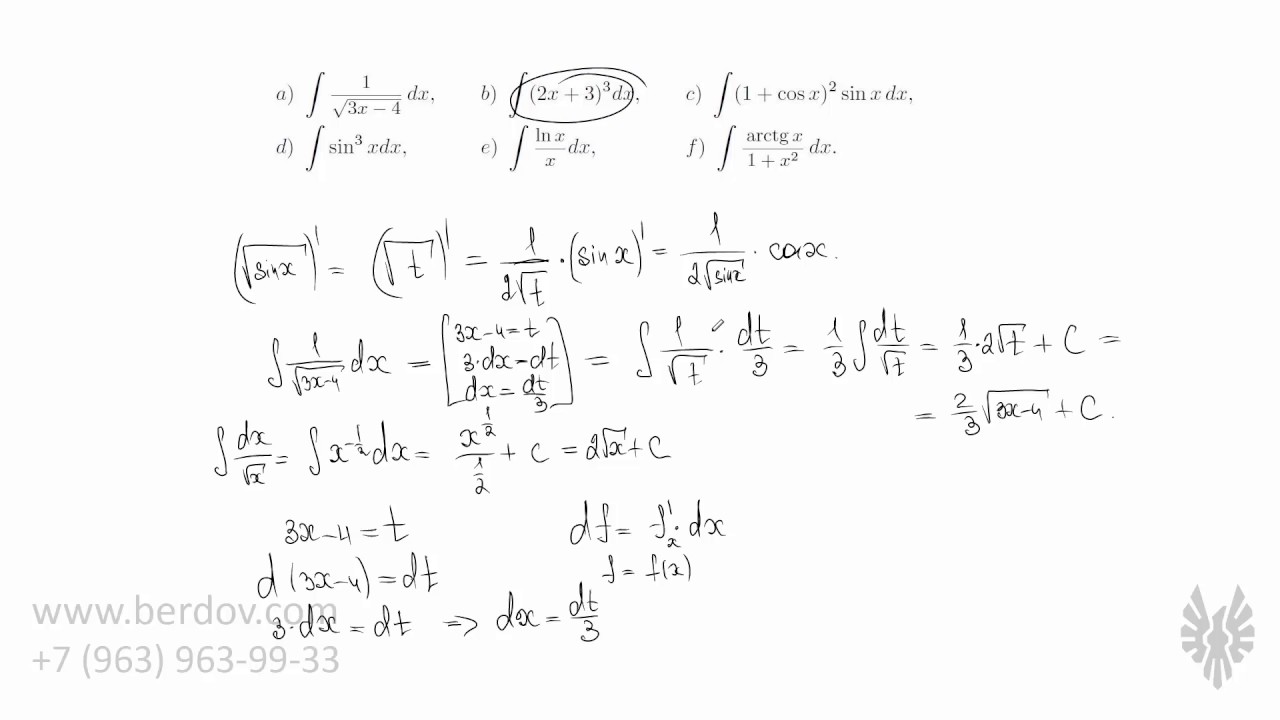Разбор задачи 14 (профильный ЕГЭ по математике). Есть доказательство и сечение пирамиды плоскостью.
Оригинал урока:
http://www.berdov.com/ege/soli....d_geometry/perimetr-

Учимся строить сечения многогранников плоскостью и использовать их для дальнейших вычислений. Так решается задача 14 из профильного ЕГЭ по математике, которая состоит из двух пунктов.

В этом видео репетитор по математике Павел Бердов решает одну из таких задач 14, которые реально могут встретиться на экзамене. Оригинал видео:
http://www.berdov.com/ege/soli....d_geometry/postroeni

Угол между плоскостями в пространстве можно найти как через графические построения, так и аналитически. Сегодня мы займёмся именно аналитическим способом, причём составлять уравнение плоскости будем через решение соответствующей системы.:)

0:00 Вступление
2:17 Решение стереометрической задачи из ЕГЭ по математике
12:11 Заключение

Оригинал видео:
http://www.berdov.com/ege/soli....d_geometry/ugol-mejd

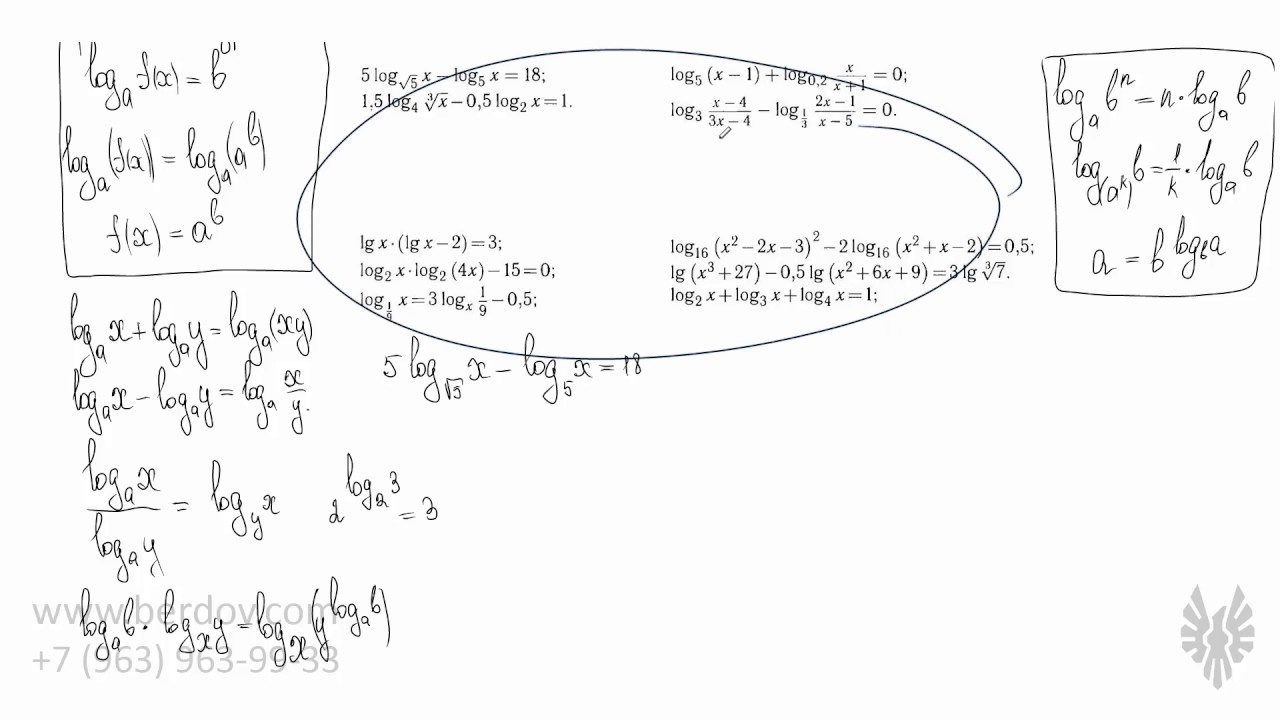
Когда мы решаем логарифмическое уравнение или неравенство, часто приходится выполнять простые на первый взгляд преобразования:
1. Внести множитель перед логарифмом в аргумент или основание логарифма;
2. Наоборот, вынести степень из аргумента или основания и поставить её как множитель перед логарифмом.

Для подобных преобразований есть специальные формулы. И эти формулы прекрасно работают, пока в аргументе и основании логарифма стоят обычные числа. Но как только там появляются переменные (или целые функции), всё становится намного интереснее.

В этом уроке мы обсудим типичные ошибки учеников, решающих подобные задачи. И рассмотрим приёмы, позволяющие избежать таких ошибок. А в качестве бонуса научимся сравнивать иррациональные числа и вписывать их в нужную нам область определения.

00:53 Простейший пример: в какой момент меняется область определения
01:50 Задание 1: сужение области определения (потеря корней)
10:01 Когда область определения, наоборот, расширяется
11:39 Задание 2: расширение области определения (лишние корни)
20:07 Сравнение иррациональных чисел
21:05 Задание 3: логарифмическое уравнение с некрасивыми корнями
33:41 Вывод: как сравнивать иррациональные числа

Это большой урок, посвящённый уравнениям с логарифмами. В нём мы пройдёмся от самых простых конструкций — типовых уравнений из учебников — до весьма хитрых задач, для решения которых потребуется внимательно изучить ОДЗ и пересекать множества на параллельных прямых.:)

Основной сайт с дополнительными материалами: https://www.berdov.com/

В этом видео мы разберём основные свойства логарифмов и научимся преобразовывать логарифмические выражения на основании этих свойств. Это один из важнейших уроков для тех, кто действительно хочет разобраться в логарифмах.

Оригинал видео и дополнительные материалы:
https://www.berdov.com/docs/lo....garithm/basic_proper

Финальный и самый главный урок. Пора перейти от теории к практике — сформулировать свою Большую цель и сделать хотя бы первый шаг к её достижению.

Основная страница урока с дополнительными материалами:
http://www.berdov.com/blog/life/bolshaya-cel/

Учимся отличать мечты от целей. И либо выкидываем мечты из своей жизни, либо переформулируем их в реальные, достижимые цели.

Основная страница урока с дополнительными материалами:
http://www.berdov.com/blog/life/celi-i-mechti/

Знакомимся с понятием технологического тупика и учимся избегать таких тупиков в своей повседневной деятельности.

Основная страница урока с дополнительными материалами:
http://www.berdov.com/blog/lif....e/krivaya-vozmojnost

Учимся отличать процесс работы от результата. И начинаем ориентироваться именно на результат.

Основная страница урока с дополнительными материалами:
http://www.berdov.com/blog/lif....e/process-i-rezultat

Первый урок тренинга. Учимся отличать факты от домыслов.

Основная страница урока с дополнительными материалами:
http://www.berdov.com/blog/life/fakti-i-domisli/

Вводное видео тренинга. В нём я расскажу, для кого этот тренинг нужен и полезен.

Основная страница урока с дополнительными материалами:
http://www.berdov.com/blog/life/vvodnij-urok/

Второй урок решаем сложны показательные уравнения. Сегодня мы разберём два новых способа решения, а заодно потренируемся на большом количестве уравнений разного уровня сложности. В целом показательные уравнения почти всегда решаются довольно просто.

Основная страница урока:
https://www.berdov.com/docs/ex....ponenta/pokazatelnie

Большой урок, посвящённый решению показательных уравнений. Под показательным мы подразумеваем любое уравнение, содержащее в себе элемента a^x или в более сложных случаях — a^f(x).

Как решать такие уравнения? Прежде всего с помощью замены переменной (показательную функцию обозначаем за величину t), а также разложением на множители и выделением устойчивого выражения. Все описанные приёмы решения показательных уравнений будут разобраны в сегодняшнем видео уроке.:)

Определённый интеграл на отрезке [a; b] — это площадь криволинейной трапеции, ограниченной осью OX, графиком функции y = f(x) и вертикальными линиями x = a и x = b. Определённый интеграл связан с неопределённым через формулу Ньютона-Лейбница. Как считать такой интеграл и какие у него свойства — об этом мы поговорим в сегодняшнем видео.:)

Дробно-рациональные функции встречаются в интеграле очень часто. Основная проблема — разнообразие первообразных, которые возникают в процессе интегрирования. Такие интегралы любят давать на самостоятельных работах и экзаменах.

Первый урок по интегралам. Разбираем теорию: что такое первообразная, что такое неопределённый интеграл, а также основные правила и приёмы интегрирования (табличные интегралы). Более специфические методы будут рассмотрены в отдельных видео.

Один из основных приёмов интегрирования — это замена переменной. Сегодня мы найдём большое количество неопределённых интегралов от самых разных функций. По сути видеоуроке будут рассмотрены два взаимодополняющих приёма: замена переменной и выделение полного дифференциала.

Произведение двух чисел положительно, если знаки множителей совпадают. И напротив: произведение отрицательно, если знаки множителей различаются. Этот факт можно использовать для решения сложных неравенств, когда метод интервалов или решение напролом уже не помогает.

Часто одним из множителей будет корень, либо модуль (иначе зачем вообще какой-то новый алгоритм?). Безусловно, для каждого из этих случаев есть собственные алгоритмы решения — они позволяют быстрее решить лёгкое неравенство, однако их эффективность быстро падает по мере усложнения задачи.

В чём преимущество алгоритма, изложенного в этом уроке? Первое — вы никогда не запутаетесь. Второе — этот алгоритм универсален. Корни, модули, а в будущем логарифмы, да хоть тригонометрия — всё решается по одной и той же схеме.

00:00 Основная идея
00:18 Простой пример: неравенство вида "произведение меньше нуля"
05:54 Как можно ускорить вычисления
10:19 Случай нестрогих неравенств
15:58 Что будет, если вместе умножения рассмотреть деление
21:51 Выводы

Домашняя работа будет сегодня чуть позже.

00:58 Что уже нужно знать
05:04 Основная схема решения рациональных неравенств
27:22 Альтернативная схема — очень полезная
49:41 Учёт кратности корней
1:20:19 Что делать, если в числителе и знаменателе обнаружены одинаковые корни
1:44:10 Особо упоротые случаи: перемножение кратностей
2:01:00 Предварительное преобразование неравенства
2:37:00 Заключение

Рациональные неравенства —это более сложная версия классических неравенств, решаемых методом интервалов. Сегодня мы детально разберём, как они решаются и какие подводные камни могут встретиться на нашем пути.