Последние
Домашняя работа:
https://www.berdov.com/docs/in....equality/metod_inter
Таймкод:
01:20 Что уже нужно знать
04:24 Что вообще такое неравенство
15:09 Основные приёмы решения неравенств
23:03 Метод интервалов для строгих неравенств
40:00 Метод интервалов для НЕстрогих неравенств
55:45 Разбираем типичные ошибки
1:15:21 Учёт кратности корней
1:29:58 Как отличить кратный корень от некратного
Метод интервалов — универсальный алгоритм для решения любых неравенств, представляющих собой произведение нескольких скобок.
Вводный урок по работе с координатами на плоскости. Сегодня мы узнаем, что такое координатная плоскость, научимся определять координаты точек на этой плоскости, а также отмечать точку с заданными координатами. Затем попробуем применить эти знания для решения задач более высокого уровня.
Содержание урока:
00:03 Повторение: координаты на прямой
09:45 Что такое координатная плоскость
21:58 Что такое абсцисса и ордината
24:15 Как отметить точку с заданными координатами
30:15 Координатные четверти
36:23 Начальные сведения о расстоянии на координатной плоскости
48:46 Заключение :)
Основной урок по теореме Виета. Содержание урока:
1. Повторение. Что такое корень уравнения и что значить решить уравнение;
2. Ключевые факты: понятие приведённого квадратного уравнения и, собственно, теорема Виета;
3. Применение теоремы Виета для отыскания корней квадратного уравнения;
4. Анализ знаков суммы и произведения корней для быстрого поиска корней;
5. Поиск делителей свободного члена для быстрого отыскания целых корней.
6. Выводы. Коротко о главном.
Продолжаю серию уроков, посвящённых теореме Виета. В этот раз мы будем применять её не просто для разложения на множители квадратного трёхчлена, а для сокращения рациональных дробей. Как известно, дробь состоит из числителя и знаменателя, каждый из которых может потребовать разложения на множители. Но в этом кроется подсказка: для дальнейшего сокращения и в числителе, и в знаменателе должен быть хотя бы один общий множитель.:)
Как быстро записать уравнение прямой y = kx + b, изображённой на графике? Быстро — это в течение 3—5 секунд.
Для этого существует специальный алгоритм:
1. Найти коэффициент b. Он равен ординате точки, в которой прямая пересекается с осью OY;
2. Взять на прямой две точки с целочисленными координатами. Построить прямоугольный треугольник и найти его катеты;
3. Пусть катеты равны DX и DY. Тогда k = DY/DX (с плюсом или минусов — зависит от того, возрастает прямая или убывает).
Пара моментов:
1. Коэффициент k может быть дробным. Алгоритм от этого не поменяется.
2. Коэффициент b тоже может быть дробным. В этом случае его можно найти с помощью коэффициента k и отступов.
А вообще уравнение прямой y = kx + b называется уравнением с угловым коэффициентом. Потому что тут явно выделен коэффициент k — в отдельном видео мы убедимся, что это тангенс угла наклона прямой к положительному направлению оси OX.
00:00 Постановка задачи: учимся находить уравнение прямой БЫСТРО
01:17 Алгоритм нахождения коэффициентов k и b
04:30 Замечание о целочисленных координатах точек
06:41 Случай дробных коэффициентов
09:33 Другой способ найти дробные коэффициенты
12:31 Как не ошибиться в применении всех этих алгоритмов
Продолжаем тему линейных уравнений. Сегодня рассмотрим пару частных случаев: когда коэффициент при переменной x равен нулю, а также когда свободное слагаемое равно нулю.
Материал для 5—6 класса. Учимся решать простейшие линейные уравнения.
В этом уроке будет совсем немного теории и очень много практики. Мы узнаем, что такое описанная окружность, какие у неё свойства, научимся работать со вписанными треугольниками и четырёхугольниками и разберём несколько действительно интересных задач.
01:52 Теория: что нужно знать про описанные окружности
29:36 Задача 1: вписанный треугольник
45:16 Задача 2: вписанный четырёхугольник
53:48 Задача 3: применение тригонометрии
01:06:09 Задача 4: взаимодействие вписанной и описанной окружности
01:15:50 Задача 5: более сложная комбинация вписанной и описанной окружности
01:23:58 Задача 6: вписанные и описанные четырёхугольники
01:34:15 Задача 7: сложная задача на четырёхугольники
01:52:26 Задача 8: введение переменных
02:03:44 Заключение
Касательная — один из самый простых (и одновременно самых нелюбимых) объектов в планиметрии. Вообще, всё, что касается окружностей, большинство учеников не любят. И правильно делают.:)
00:00:06 Вводная теоретическая часть
00:15:30 Простейшие задачи
00:35:57 Формирование касательных из условия
00:51:16 Взаимодействие касательной и секущей
01:00:33 Общие касательные двух окружностей — 1
01:10:22 Общие касательные двух окружностей — 2
01:30:05 Описанные многоугольники
01:40:35 Более сложные приложения (теорема косинусов)
01:53:09 Заключение
Сегодня мы рассмотрим все ключевые свойства касательной, которые нужно знать. А заодно решим кучу задач. Также вы можете скачать домашнюю работу на сайте:
https://www.berdov.com/docs/ok....rujnost/chto-takoe-k
Большой урок, посвящённый определителям матриц и их вычислению.
01:24 Краткая вводная. Что надо знать о матрицах
05:38 Геометрическое определение определителя
11:57 Алгебраическое определение определителя
36:20 Практика. Матрицы 2x2 и 3x3
48:10 Миноры и алгебраические дополнения
59:01 Теорема Лапласа
1:04:29 Разложение определителя по строке (столбцу)
1:15:40 Основные свойства определителей
1:25:19 Матрицы 4х4
1:44:40 Уравнения и неравенства с определителями
Определитель — одно из центральных понятий всей алгебры матриц (а заодно и векторной алгебры, но не будем о грустном). Что это такое? Как правильно считать определители? И какие у них свойства? Обо всём этом мы подробно поговорим в сегодняшнем уроке.
https://www.berdov.com/works/m....atrix/opredelitel-ma
Домашку и ответы можно скачать на сайте:
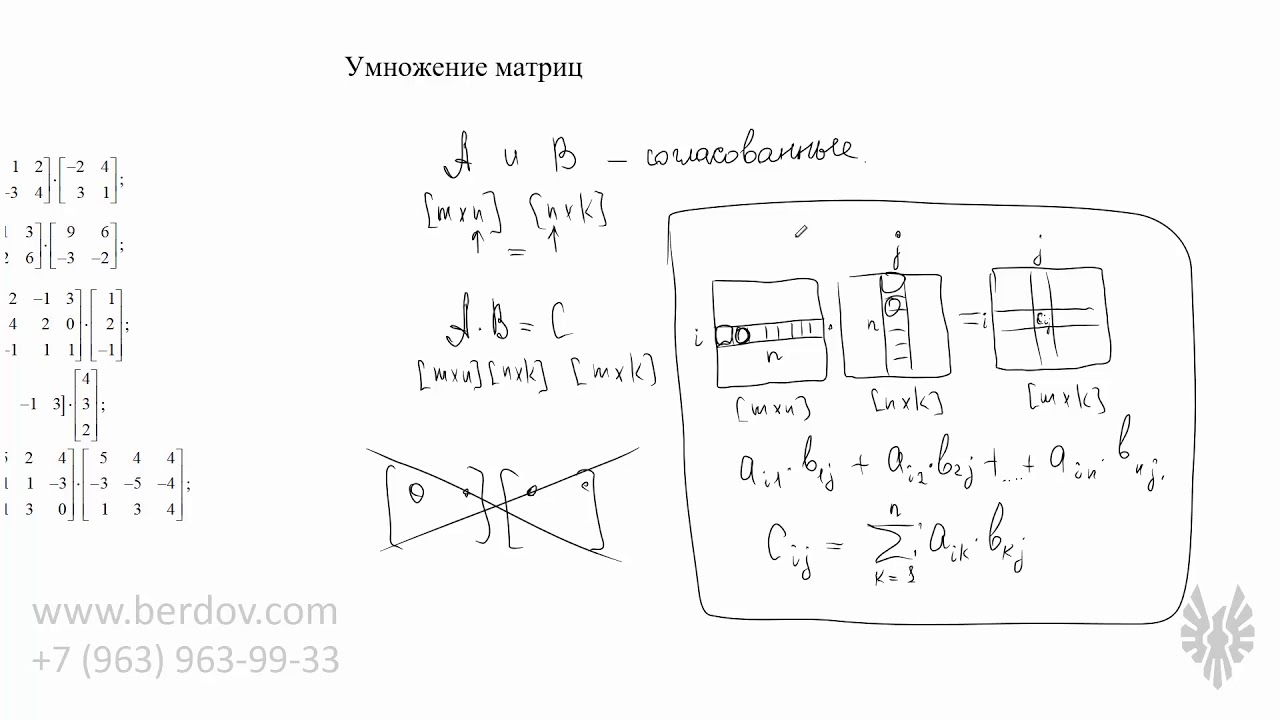
https://www.berdov.com/works/m....atrix/umnozhenie-mat
Умножение матриц в алгебре — одна из ключевых и одновременно одна из самых мозговыносящих операций. Матрицы должны быть согласованы, умножение не коммутативно, у него куча странных эффектов и т.д. Обо всём этом сегодня и поговорим.:)
00:06 Вступление
03:37 Повторение: сложение матриц и умножение на число
06:41 Определение умножения матриц
20:44 Вектор-столбцы и вектор-строки
27:32 Возведение матрицы в степень
39:55 Практика: разные матрицы
Домашку можно скачать здесь:
https://www.berdov.com/works/m....atrix/obratnaya-matr
Обратная матрица порядка n — это такая матрица B, которая при умножении на исходную матрицу A даёт единичную E. Она определена для невырожденных матриц и всегда одна.
00:39 Определение обратной матрицы
05:06 Условия существования и единственность
15:22 Теорема об обратной матрице (основной способ нахождения)
43:04 Второй способ — через присоединённую матрицу E
1:11:29 Ещё раз об элементарных преобразованиях
1:12:29 Приложение: матричные уравнения
Домашка на подходе.:)
Этот урок — своего рода шпаргалка для тех, кто хочет разобраться в тригонометрии на прямоугольном треугольнике. Мы не только вспомним что такое синус, косинус, тангенс и котангенс, но и потренируемся в их применении для нахождения сторон треугольника.
Попутно вспомним важнейшие теоремы и определения:
1. Теорема Пифагора — тригонометрия в ОГЭ точно не обходится без неё;
2. Подобные треугольники — причина и одновременно следствие классической тригонометрии;
3. Касательные, секущие и хорды в окружности, а также их полезные свойства;
4. Плавный переход к серьёзной тригонометрии на единичном круге.
Итого получился максимально полезный урок как для 9, так и для 11 класса.:)
00:21 Основные факты из тригонометрии на прямоугольном треугольнике
01:42 Задание 1: учимся дополнять чертёж до прямоугольного треугольника
04:37 Теорема Пифагора и её связь с тригонометрией
06:07 Задание 2: классическая задача на решение треугольника
13:21 Задание 3: высота в прямоугольном треугольнике
21:03 Что такое подобные треугольники
22:36 Задание 4: доказываем подобие треугольников
27:37 Окружность, касательные и хорды
29:21 Задание 5: теорема о касательной и секущей к окружности
36:53 Задание 6: сложная тригонометрия в текстовой задаче
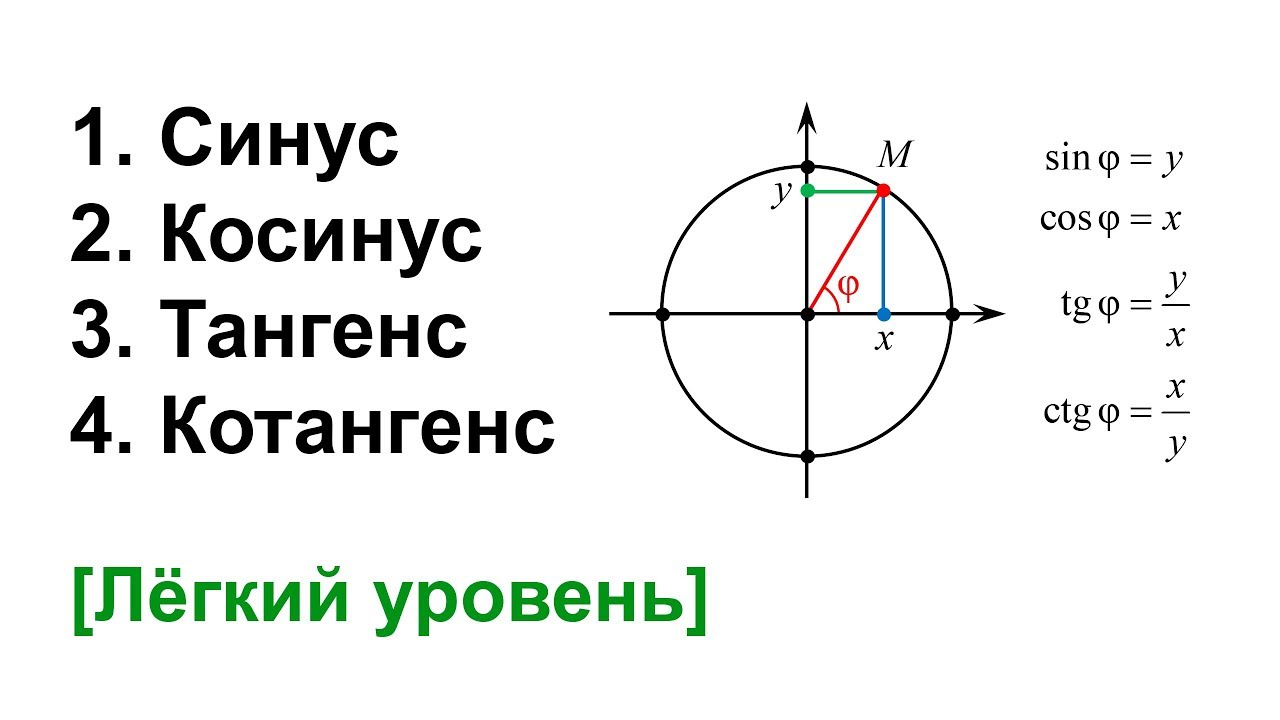
Этот урок — ключевой во всей «взрослой» тригонометрии. Мы узнаем, как с помощью тригонометрического круга найти синус, косинус, тангенс и котангенс для любого угла, выраженного в радианах. Познакомимся с тем, как строить оси тангенсов и котангенсов. А заодно составим таблицы важнейших значений тригонометрических функций и изучим парочку их свойств.
Определение синуса, косинуса, тангенса и котангенса через тригонометрический круг — это момент, разделяющий привычную там тригонометрию в прямоугольном треугольнике и алгебраическую тригонометрию, которой мы будем заниматься в 10—11 классах. На основе этих определений возникнет целый класс задач: тригонометрические уравнения и неравенства, изучение возрастания и убывания тригонометрических функций, их периодичность и т.д.
Но всё это будет чуть позже. Сегодня наша задача — просто научиться считать синус, косинус, тангенс и котангенс любого угла.:)
00:03 Краткая вводная: о чём речь
01:48 Что уже надо знать
06:53 Синус, косинус, тангенс и котангенс острого угла
18:39 Таблица синусов и косинусов
21:53 Примеры вычислений
30:02 Синус, косинус, тангенс и котангенс произвольного угла
37:37 Ось тангенсов и котангенсов
45:43 Замечание по этим осям
47:00 Составляем таблицу тангенсов и котангенсов с помощью осей
53:29 Чётность и нечётность
01:02:53 Практикум
01:10:44 Выводы и соображения на будущее
Две частицы, имеющие массу m и заряд q, находятся в вершинах равностороннего треугольника, составленного из лёгких нитей длиной l. Систему поднимают вертикально вверх с ускорением а, равным по модулю g. Определите натяжение нити, соединяющей частицы.
Тригонометрический круг — это просто единичная окружность с центром в начале координат. На ней специальным образом чертят углы, стороны которых высекают на окружности дуги, равные радианной мере. На этом строится вся #тригонометрия в старших классах и университетской математике.
Из этого урока вы узнаете, что такое тригонометрический круг и как с ним работать. Более конкретно:
1. Определение (приведено выше);
2. Как отмечать точки на тригонометрическом круге;
3. Как искать координаты этих точек;
4. Как выполнять обратную операцию: описывать все точки с заданными координатами.
Эти материалы позволят вам легко разобраться во всей «взрослой» тригонометрии. А рассматриваемые приёмы уже сейчас позволят решать множество тригонометрических задач.
00:03 Повторение: радианная мера угла
03:47 Что такое тригонометрический круг
09:11 Ещё раз: что надо знать
10:51 Алгоритм: как построить точку на круге, зная угол
20:08 Замечание 1: центральная и осевая симметрия
21:08 Замечание 2: вспомогательный квадрат
22:25 Замечание 3: правильное оформление выкладок
23:24 Алгоритм: как найти координаты точки на круге
38:35 Первые сведения о периодичности
41:26 Нахождение углов по координатам
Этот урок относится к лёгкому уровню. Чуть позже будет опубликовано ещё одно видео по тригонометрическому кругу, где мы разберём более сложные вопросы: что делать с «некрасивыми» углами, как ведут себя точки на окружности при небольших углах поворота и т.д.