Обычно при решении тригонометрических уравнений получаются красивые корни и табличные значения. Но что делать, если получился какой-нибудь арктангенс? Как в этом случае грамотно отобрать корни на отрезке и не допустить обидных ошибок?

0:00 Описание проблемы: сложные тригонометрические уравнения в ЕГЭ по математике
0:41 Решение сложной задачи 13 из профильного ЕГЭ
2:24 Учёт области определения корня и тангенса
12:41 Как отмечать арктангенсы на тригонометрической окружности
14:47 Отбор корней уравнения на указанном отрезке
21:48 Проверка правильности решения
27:17 Ключевые выводы и факты

http://www.berdov.com/ege/equa....tion-root/arktangens

Решение тригонометрического уравнения в задаче 13 из профильного ЕГЭ по математике 2016. Отбор корней на отрезке графическим методом. Учимся применять формулы тригонометрии (синус двойного угла), а также используем замену переменной. Типичная задача из ЕГЭ.

0:00 Вступление, описание тригонометрических уравнений в ЕГЭ
по математике
0:34 Решение тригонометрической задачи из профильного ЕГЭ
2:20 Отбор корней уравнения на указанном отрезке
10:17 Заключение и рекомендации для учеников

http://www.berdov.com/ege/equa....tion-root/reshenie-u

Решение тригонометрических уравнений из ЕГЭ по математике 2016. Отбор корней на отрезке. Формула понижения степени в тригонометрии и её применение для решения уравнений.

0:00 Введение. Общие принципы решения тригонометрических уравнений с ограничением;
16:02 — Пример решения 1-го уравнения с корнем;
38:30 — Ещё один пример — более простой;
48:26 — Формула понижения степени в тригонометрическом уравнении;
59:36 — Заключение и повторение основных формул.

Оригинал урока:
http://www.berdov.com/docs/tri....gonometriya/uchet-og

Как решать показательные неравенства? Существует несколько методов — от простейших конструкций до всевозможных группировок и разложения на множители. Сегодня мы познакомимся с основными способами решения показательных неравенств и формулами преобразований.

Основной урок:
https://www.berdov.com/docs/ex....ponenta/reshenie-pok

В этом уроке мы продолжаем учиться решать логарифмические неравенства методом рационализации с привлечением других приёмов.

Оригинал видео:
http://www.berdov.com/docs/log....arithm/reshenie-loga

Метод математической индукции — это приём доказательства утверждений, зависящих от натурального параметра. Он состоит из трёх шагов:
1. Доказать утверждение для конкретных n. Например, для n = 1 или n = 2;
2. Предположить, что утверждение верно для n = k;
3. На основе этого предположения доказать, что утверждение верно для n = k + 1.

Если все три шага выполнены, то исходное утверждение будет доказано для всех натуральных чисел n. Это позволяет доказывать сложные и нестандартные формулы.

Сегодня мы будем тренироваться в применении метода мат. индукции на четырёх задачах: два равенства и два неравенства. Заодно повторим несколько важных фактов из теории тождеств и, собственно, неравенств.

00:00 Метод математической индукции на примере простой задачи
04:16 Более сложная задача, анализ формулы последнего слагаемого
08:17 Доказательство рациональных неравенств (больная тема для многих)
12:49 Доказательство иррациональных неравенств (вспоминаем квадратные корни)

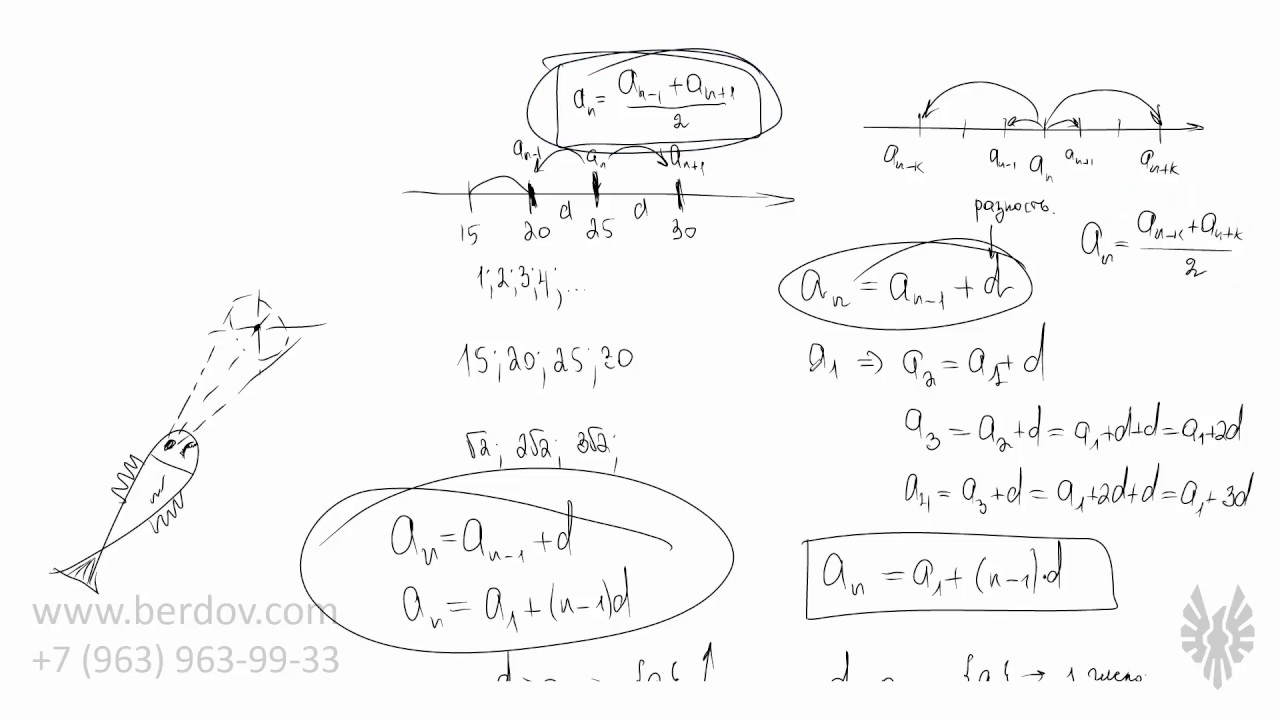
Это самый первый и самый важный урок по прогрессиям. Разбираем, что такое арифметическая прогрессия, какие у неё свойства, а заодно решаем кучу задач по прогрессиям.

Основная страница урока — там вы можете скачать задачи для самостоятельного решения и проверить себя:
https://www.berdov.com/docs/pr....ogressiya/chto-takoe

Более сложная версия предыдущей задачи — здесь требуется найти суммарные выплаты в течение второго года. Это одна из экономических задач 17 в ЕГЭ по математике 2016. Решается с помощью формул арифметической прогрессии.

Оригинал видео:
http://www.berdov.com/ege/cred....it/kredit-plyus-proc

Решение задач на арифметическую прогрессию. Вычисление n-го элемента арифметической прогрессии. Использование формул, первого элемента и разности прогрессии.

http://www.berdov.com/docs/pro....gressiya/prosteyshie

В этом видео мы познакомимся с новым объектом — арифметической прогрессией. Что такое арифметическая прогрессия? И как с ней работать. Как складывать её элементы и какие формулы для этого существуют? Об этом и поговорим.:)

Оригинал урока:
http://www.berdov.com/docs/pro....gressiya/chto-takoe-

Прямая трансляция вебинара по прогрессиям

В этом видео мы познакомимся с геометрической прогрессией. Что такое геометрическая прогрессия? Какие формулы есть для работы с ней, как складывать её элементы и т.д. — об этом и поговорим.:)

Оригинал видео:
http://www.berdov.com/docs/pro....gressiya/chto-takoe-

Немного нестандартное задание 15 из профильного ЕГЭ по математике: комбинация модулей, многочленов и показательных функций. Если решать такие задачи напролом, можно утонуть в вычислениях. Поэтому сегодня мы рассмотрим довольно интересный приём, многократно ускоряющий решение.

00:05 Краткая вводная: модуль числа и свойства, которые надо знать
02:30 Собственно, задача
07:00 Применяем метод группировки
08:45 Главная фишка: переходим от неравенства к СИСТЕМЕ уравнений
12:35 Числовая прямая и сравнение иррациональных чисел
13:47 Заключение: ещё раз перечисляем все ключевые идеи

Решение сложного неравенства из ЕГЭ-2017 по математике, которое содержит модуль и логарифм. Очень интересная задача: в ней одной по сути собрано всё, что нужно знать для решения любой другой задачи 15.:)

В этом видео мы разберём типичную задачу 15, которая вполне может встретиться в ЕГЭ-2017 по математике. Как вы знаете, теперь за это задание дают всего 2 первичных балла — неравенства стали проще, но методы и технологии решения остались прежними.

Одна из ключевых сложностей логарифмических неравенств — это сравнение иррациональных корней. В этом видео мы научимся сравнивать корни разных видов из ОДЗ и решения неравенств.

Одна из самых сложных задач — это когда функция возводится в степень-функцию. Такие примеры на ЕГЭ-2017 вряд ли попадутся, но их нужно уметь решать для подстраховки. Поэтому предлагаю вашему вниманию подробное решение системы неравенств из задания 15.:)

Решение логарифмического неравенства методом рационализации. Подробный разбор каждого шага. Пересечение корней на параллельных прямых и учёт области определения.

0:00 Вступление, общее пояснение поставленной задачи
0:36 Решение логарифмического неравенства с переменным основанием
2:49 Пересечение множеств на параллельных осях — очень важный навык
4:20 Заключение, краткое резюме по логарифмическим неравенствам

http://www.berdov.com/docs/log....arithm/logarifmiches

Решение логарифмических неравенств и систем методом интервалов. Решение задачи 15 из профильного ЕГЭ по математике 2016.

Метод интервалов — очень эффективный инструмент. Когда неравенство с логарифмами не сводится к простейшему каноническому, метод рационализации (специфический инструмент именно для логарифмов) перестаёт работать. И вот тогда мы подключаем тяжёлую артиллерию в виде метода интервалов.:)

0:00 Вступление, общая характеристика задач 15 с логарифмами из ЕГЭ по математике
0:45 Решение логарифмического неравенства методом интервалов
10:05 Решение показательного неравенства методом рационализации
12:47 Пересечение множеств с помощью параллельных прямых
13:46 Ключевые выводы и моменты видеоурока: что нужно знать о задачах из ЕГЭ?

http://www.berdov.com/ege/sist....ema-neravenstv/metod

Довольно интересное задание 16 из профильного ЕГЭ по математике. Для её решения надо вспомнить, что:
1. Трапеция, вписанная в окружность, всегда равнобедренная;
2. Вписанные углы, опирающиеся на равные хорды одной и той же окружности, равны. При этом хорды могут располагаться в произвольном месте этой окружности;
3. Пересекающиеся хорды делятся точкой пересечения на отрезки, произведения которых равны.

Зачем всё это? Да просто чтобы доказать равенство двух отрезков. А затем надо будет посчитать площадь вписанного пятиугольника, для чего придётся привлекать теорему косинусов, но это уже совсем другая история.:)

00:03 Свойства хорд и окружностей
03:48 Задание 16 из ЕГЭ, пункт А: доказательство
20:07 Задание 16 из ЕГЭ, пункт Б: площадь пятиугольника
28:37 Заключение