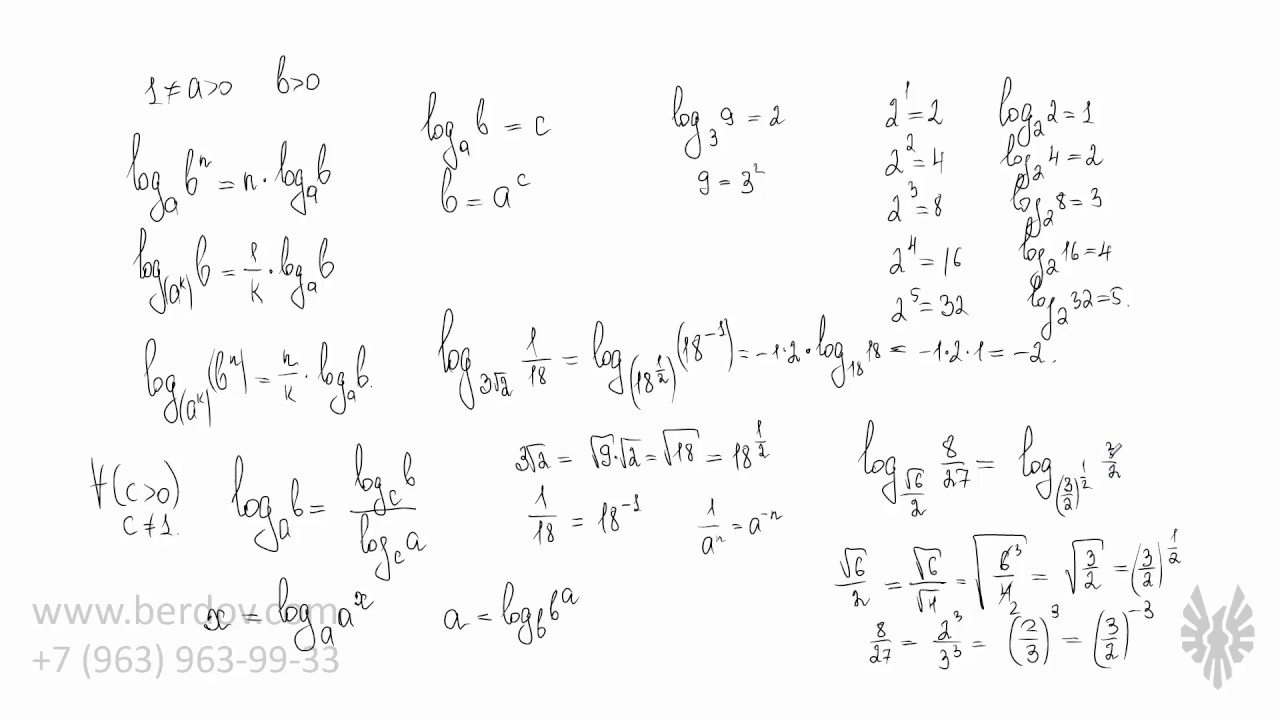Решение логарифмического неравенства методом рационализации. Подробный разбор каждого шага. Пересечение корней на параллельных прямых и учёт области определения.

0:00 Вступление, общее пояснение поставленной задачи
0:36 Решение логарифмического неравенства с переменным основанием
2:49 Пересечение множеств на параллельных осях — очень важный навык
4:20 Заключение, краткое резюме по логарифмическим неравенствам

http://www.berdov.com/docs/log....arithm/logarifmiches

Решение логарифмических неравенств и систем методом интервалов. Решение задачи 15 из профильного ЕГЭ по математике 2016.

Метод интервалов — очень эффективный инструмент. Когда неравенство с логарифмами не сводится к простейшему каноническому, метод рационализации (специфический инструмент именно для логарифмов) перестаёт работать. И вот тогда мы подключаем тяжёлую артиллерию в виде метода интервалов.:)

0:00 Вступление, общая характеристика задач 15 с логарифмами из ЕГЭ по математике
0:45 Решение логарифмического неравенства методом интервалов
10:05 Решение показательного неравенства методом рационализации
12:47 Пересечение множеств с помощью параллельных прямых
13:46 Ключевые выводы и моменты видеоурока: что нужно знать о задачах из ЕГЭ?

http://www.berdov.com/ege/sist....ema-neravenstv/metod

Довольно интересное задание 16 из профильного ЕГЭ по математике. Для её решения надо вспомнить, что:
1. Трапеция, вписанная в окружность, всегда равнобедренная;
2. Вписанные углы, опирающиеся на равные хорды одной и той же окружности, равны. При этом хорды могут располагаться в произвольном месте этой окружности;
3. Пересекающиеся хорды делятся точкой пересечения на отрезки, произведения которых равны.

Зачем всё это? Да просто чтобы доказать равенство двух отрезков. А затем надо будет посчитать площадь вписанного пятиугольника, для чего придётся привлекать теорему косинусов, но это уже совсем другая история.:)

00:03 Свойства хорд и окружностей
03:48 Задание 16 из ЕГЭ, пункт А: доказательство
20:07 Задание 16 из ЕГЭ, пункт Б: площадь пятиугольника
28:37 Заключение

Эту задачу я увидел сразу после досрочного ЕГЭ 2019, хотя никакого отношения к досрочнику она не имеет. Многие ученики не знают, как подступиться к задачам на доказательство свойств точек (в отличие от свойств отрезков — там обычно всё понятно).

Поэтому внимательно посмотрите данное видео, чтобы в будущем, когда столкнётесь с подобными задачами, не возникло проблем. Но в целом рекомендация проста: доказательство каких-либо свойств точек рекомендуется сводить к свойствам отрезков и определениям. Как? Об этом сегодня и поговорим.:)

00:05 Краткая вводная: основные принципы доказательства
03:57 Собственно, задача — разбираем пункт А.
21:42 Замечание по поводу вписанных окружностей
22:30 Решение задачи — разбираем пункт Б.
30:27 Важное замечание о прямоугольных треугольниках

Решение задачи 16 из профильного ЕГЭ по математике 2019 по планиметрии: разбор доказательства с трапецией и равнобедренным треугольником.

Решение задачи 16 из профильного ЕГЭ по математике 2017. В задаче присутствуют окружности и касательные. Разумеется, вся задача строится вокруг доказательства утверждения в планиметрии.

Задача 16 решается зачастую очень просто, если правильно сделать чертёж. Сегодня мы разберём довольно сложную задачу 16 нового вида (доказательство и вычисление), которая помимо грамотного чертежа требует ещё и знания формул площади, а также свойств вписанных углов и касательных к окружности. Получается, что в одной задаче сосредоточен практически весь математический инструментарий, который изучают в 8—9 классах.:)

Тригонометрия вообще является универсальным инструментом в задачах 16 из профильного ЕГЭ по математике. Но зачастую она является чуть ли ни единственным способом решения. Пример такой задачи мы сегодня и рассмотрим.

Теорема косинусов для нахождения сторон треугольника. Использование подобия треугольников для решения сложных планиметрических задач.

0:00 Вступление, формулировка теоремы косинусов
1:02 Решение задачи с помощью теоремы косинусов
5:37 Комментарий по поводу неоднозначности чертежа

Видео будет полезно тем, кто готовится к ЕГЭ или ОГЭ по математике. А также всем, кто хочет научиться применять теорему косинусов в реальных задачах.

Оригинал видео:
http://www.berdov.com/docs/tre....ugolnik/teorema-kosi

Решение стереометрической задачи (задание 14) из ЕГЭ-2017 по математике. Задача разбита на 2 части: доказательство и вычисление объёма пирамиды. В любом случае, помните: стереометрия всегда сводится к планиметрии с помощью углов и перпендикуляров. Именно такой подход мы и будем использовать для решения данной задачи.:)

Ещё одна задача 14. Учимся считать угол между плоскостями. Строго говоря, его можно считать методом координат или напрямую.
Оригинал видео:
http://www.berdov.com/ege/soli....d_geometry/ugol-mejd

Разбираем задание 14 из ЕГЭ по математике. Площадь сечения многогранника плоскостью — один из самых часто встречающихся типов задач.

Оригинал урока:
http://www.berdov.com/ege/soli....d_geometry/ploshad-s

Разбор задачи 14 (профильный ЕГЭ по математике). Есть доказательство и сечение пирамиды плоскостью.
Оригинал урока:
http://www.berdov.com/ege/soli....d_geometry/perimetr-

Учимся строить сечения многогранников плоскостью и использовать их для дальнейших вычислений. Так решается задача 14 из профильного ЕГЭ по математике, которая состоит из двух пунктов.

В этом видео репетитор по математике Павел Бердов решает одну из таких задач 14, которые реально могут встретиться на экзамене. Оригинал видео:
http://www.berdov.com/ege/soli....d_geometry/postroeni

Угол между плоскостями в пространстве можно найти как через графические построения, так и аналитически. Сегодня мы займёмся именно аналитическим способом, причём составлять уравнение плоскости будем через решение соответствующей системы.:)

0:00 Вступление
2:17 Решение стереометрической задачи из ЕГЭ по математике
12:11 Заключение

Оригинал видео:
http://www.berdov.com/ege/soli....d_geometry/ugol-mejd

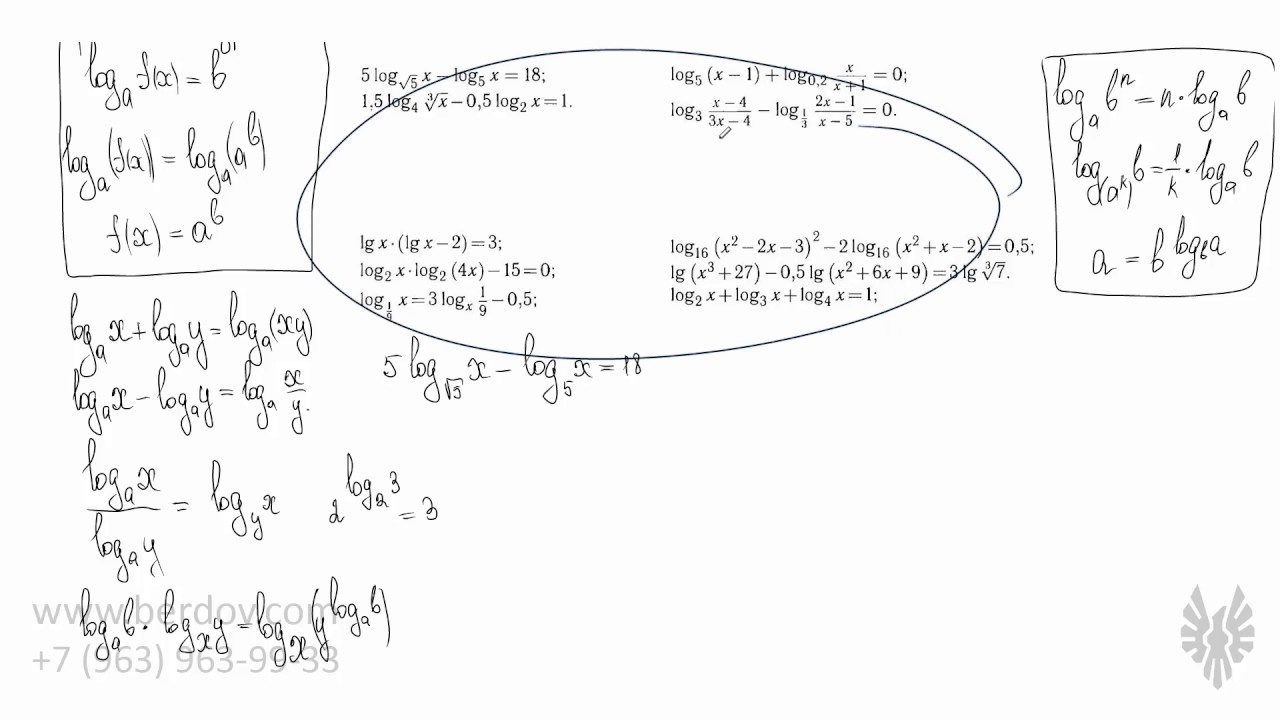
Когда мы решаем логарифмическое уравнение или неравенство, часто приходится выполнять простые на первый взгляд преобразования:
1. Внести множитель перед логарифмом в аргумент или основание логарифма;
2. Наоборот, вынести степень из аргумента или основания и поставить её как множитель перед логарифмом.

Для подобных преобразований есть специальные формулы. И эти формулы прекрасно работают, пока в аргументе и основании логарифма стоят обычные числа. Но как только там появляются переменные (или целые функции), всё становится намного интереснее.

В этом уроке мы обсудим типичные ошибки учеников, решающих подобные задачи. И рассмотрим приёмы, позволяющие избежать таких ошибок. А в качестве бонуса научимся сравнивать иррациональные числа и вписывать их в нужную нам область определения.

00:53 Простейший пример: в какой момент меняется область определения
01:50 Задание 1: сужение области определения (потеря корней)
10:01 Когда область определения, наоборот, расширяется
11:39 Задание 2: расширение области определения (лишние корни)
20:07 Сравнение иррациональных чисел
21:05 Задание 3: логарифмическое уравнение с некрасивыми корнями
33:41 Вывод: как сравнивать иррациональные числа

Это большой урок, посвящённый уравнениям с логарифмами. В нём мы пройдёмся от самых простых конструкций — типовых уравнений из учебников — до весьма хитрых задач, для решения которых потребуется внимательно изучить ОДЗ и пересекать множества на параллельных прямых.:)

Основной сайт с дополнительными материалами: https://www.berdov.com/

В этом видео мы разберём основные свойства логарифмов и научимся преобразовывать логарифмические выражения на основании этих свойств. Это один из важнейших уроков для тех, кто действительно хочет разобраться в логарифмах.

Оригинал видео и дополнительные материалы:
https://www.berdov.com/docs/lo....garithm/basic_proper

Финальный и самый главный урок. Пора перейти от теории к практике — сформулировать свою Большую цель и сделать хотя бы первый шаг к её достижению.

Основная страница урока с дополнительными материалами:
http://www.berdov.com/blog/life/bolshaya-cel/

Учимся отличать мечты от целей. И либо выкидываем мечты из своей жизни, либо переформулируем их в реальные, достижимые цели.

Основная страница урока с дополнительными материалами:
http://www.berdov.com/blog/life/celi-i-mechti/