Довольно интересная задача 18 с параметром из ЕГЭ по математике — решается с привлечением как графических методов, так и аналитических. По факту всё решение сводится к разбору взаимного расположения окружностей на координатной плоскости и решению нескольких уравнений с модулем.

Продолжаем наш марафон. Сегодня мы разберём задание 18 — это задача с параметром, которая решается графически. В целом ничего сложного, однако это одна из тех задач, где нас пытаются "взять на понт" — дают дополнительное условие, усложняющее исходные уравнения, которое, однако, никак не влияет на ответ. Так что не стоит бояться сложных формул: зачастую за ними скрывается простое и лаконичное решение.:)

Страница урока на сайте:
https://www.berdov.com/ege/par....ametr/novie-zadachi-

Графическое решение задач с параметром из ЕГЭ хорошо тем, что зачастую даёт наглядный ответ. Однако иногда условие составлено таким образом, что определить точку пересечения/касания графиков "на глаз" невозможно.

В этом случае необходимы дополнительные исследования графика функции, содержащей параметр. И на помощь нам приходят производные, а также неравенства.:)

Основная страница урока:
https://www.berdov.com/ege/par....ametr/primenenie-pro

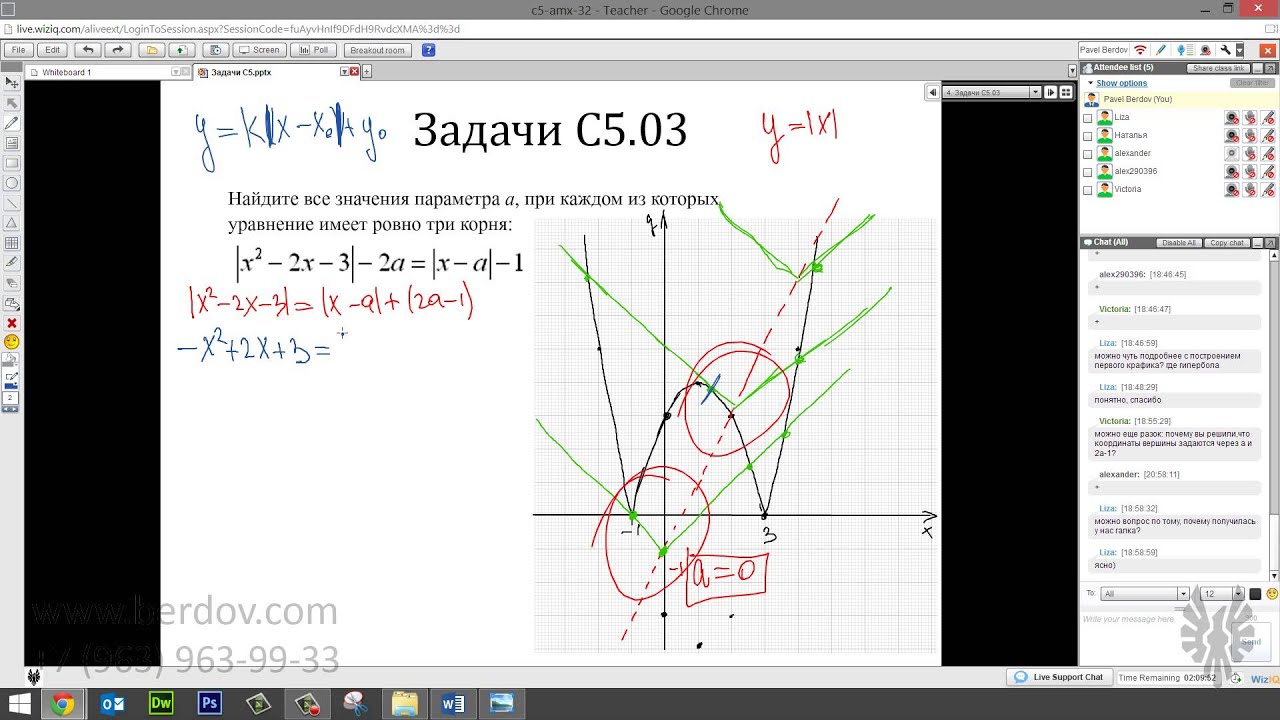
Модуль в задачах с параметром — это своеобразная "визитная карточка" профильного ЕГЭ. И если под модулем стоит лишь функция от x, многие ученики вполне справляются с заданием. Но когда под модуль ставят разные переменные, связанные с собой на графике, многие впадают в ступор.:)

Сегодня мы разберём именно такую задачу 18 — здесь графическое решение и поиск параметра будет сопровождаться построением сложных конструкций, содержащих модуль.

Задачи с параметром, содержащие модули, зачастую кажутся сложными и "неподъёмными" для многих учеников. На самом деле существует универсальный алгоритм работы с модулем: приравниваем подмодульное выражение к нулю, разбиваем прямую (или плоскость) на области с постоянным знаком, а затем просто рисуем полученный график. При этом, как и любая другая задача 18, подобная схема требует грамотной интерпретации исходного условия.

Разбор одной из самых сложных (на первый взгляд) задачи 18, которая решается графическим способом. Часто бывает так, что самые навороченные и непонятные выражения на практике разбираются очень и очень просто, если грамотно интерпретировать их графический смысл.

Довольно мозговыносящая задача (на первый взгляд), которая хорошо решается с привлечением графических и аналитических инструментов. Велика вероятность, что что-то подобное будет на ЕГЭ-2017.:)

Это отличная задача, которую недавно давали в Москве на пробном ЕГЭ по математике. Классическая задача с параметром, которая решается графически с привлечением дополнительных построений.

Продолжаем разбирать сложные и нестандартные задания 18 из профильного ЕГЭ по математике 2017. Эта задача с параметром решается графически, однако стандартные приёмы в духе "начертим график и найдём пересечение" здесь не работает — прежде всего потому что неясно, как этот график чертить.

Такие задачи всегда решаются с привлечением дополнительных геометрических соображений. По меркам ЕГЭ они считаются довольно сложными, поэтому вероятность встретить что-то подобное на настоящем экзамене невелика. Однако знать, как такое решать, совершенно необходимо.:)

Один из самых противных типов 18-го задания: нужно на графике вычертить отрезок (к тому же, с переменным "хвостом"), а затем понять, как этот отрезок может пересекаться с другими линиями, обозначенными в условии. Решается строго графически с привлечением приёмов алгебры 10 и даже 9 классов.:)

Метод областей — один из основных приёмов для решения задач 18. Когда под модулем стоит несколько переменных, лучше всего использовать графическое решение.

Решение задач с параметром. Подготовка к ЕГЭ 2016 по математике. Разбор пробного ЕГЭ 3 марта 2016 года. Графическое решение уравнений. Оригинал урока:
http://www.berdov.com/ege/para....metr/probnik-3-marta

Решение нестандартных задач с параметром, где требуется, чтобы корни составляли отрезок, в т.ч. указанной длины.

UPD. На 18:06 допущена ошибка: при перенесении слагаемого 1/2 вправо я забыл поставить минус. В результате получилось, что a = -5/4, хотя должно быть a = -9/4. В остальном решение правильное.:)

Оригинал видео:
http://www.berdov.com/docs/par....ametr/specialnie-usl

Сегодня мы разберём задачу с параметром, содержащую модуль, которая в итоге решается и с применением аналитических методов. и графически. Это так называемые комбинированные задачи — они не очень сложны, но при невнимательной работе весьма коварны.:)

Оригинал урока:
http://www.berdov.com/docs/par....ametr/grafik-modulya

Оригинал взят отсюда:
http://www.berdov.com/ege/para....metr/parametr-grafic

Математика — это просто. Приходите на занятия и убедитесь в этом сами: http://www.berdov.com

http://www.berdov.com/ege/para....metr/uravnenie-okruj

В этом видеоуроке репетитор по математике Павел Бердов решает реальную задачу C5 из ЕГЭ по математике с подробным объяснением каждого шага. Кроме того, в задаче присутствует сразу несколько «подводных камней», на которые обращается отдельное внимание.

http://www.berdov.com/ege/para....metr/okrujnost-modul

Это реальная задача C5 из ЕГЭ по математике, которая решается очень легко, если знать парочку приемов работы с графиками функций. В противном случае решение оказывается крайне сложным и проблематичным.

http://www.berdov.com/ege/para....metr/okrujnost-modul
Это одна из тех задач С5, которые, во-первых, действительно могут встретиться на ЕГЭ по математике. А во-вторых, многие ученики считают такие задачи чересчур сложными. В частности, из-за того, что в системе уравнений присутствует сразу два параметра.
Однако если вы посмотрите это видео, то лично убедитесь: при графическом подходе решать задачи с двумя параметрами оказывается очень и очень просто. Поэтому смело берите на вооружение данный прием и сдавайте ЕГЭ по математике на «отлично».

Иногда в задании 13 ЕГЭ по математике встречается такое тригонометрическое уравнение, которое нельзя решить напролом — сведением к sin x = a. Тогда к делу подключаются нестандартные приёмы:
1. Оценка левой и правой части (метод мажорант);
2. Исследование возрастания/убывания функции;
3. Разложение на множители и т.д.

Но сегодня не об этом. Сегодня мы попробуем решить эту задачу стандартными методами алгебры, которые работают не только в тригонометрии, но именно в тригонометрии они дают неожиданные результаты. О чём именно пойдёт речь? Смотрите видео — и обязательно берите на вооружение.:)

00:03 Краткая вводная: основная идея решения
05:10 Задание 13
10:40 Пункт А — решаем уравнение
17:07 Пункт Б — отбираем корни
25:04 Заключение: ещё раз о главной идее решения