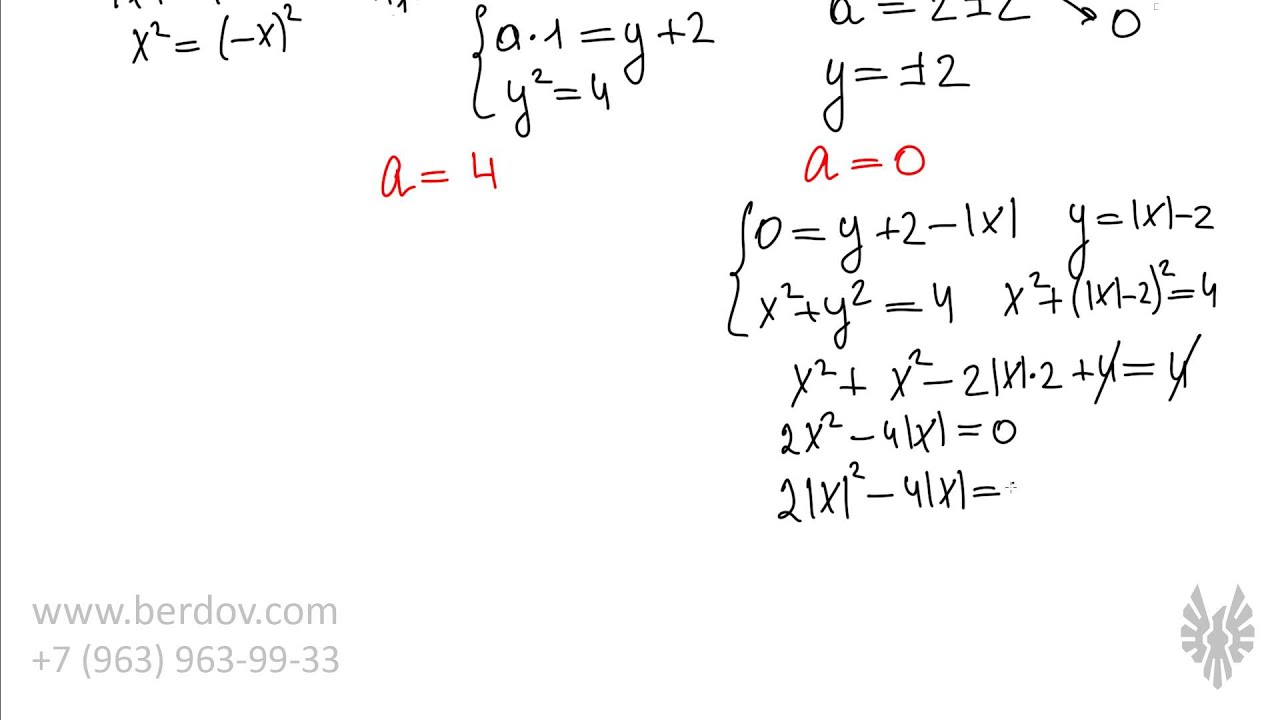http://www.berdov.com/docs/rad....ikal/irracionalnoe-n

Продолжаем изучать иррациональные неравенства вида «корень больше функции». В этот раз рассмотрим общую схему решения таких задач, а заодно познакомимся с очень эффективным инструментом для самопроверки — прилеганием корней к разделяющему числу.

http://www.berdov.com/docs/rad....ikal/irracionalnoe-n

Этим видео я начинаю серию уроков, посвященных решению неравенств вида «корень больше функции».
Для начала мы рассмотрим общие теоретические принципы, на которых строится решение подобных неравенств. Ну, а в следующих уроках будем решать более сложные задачи, требующие аккуратного и вдумчивого подхода.

Продолжаем изучать устойчивые выражения. В предыдущем уроке мы рассмотрели совсем простые задачи (впрочем, последняя задача была довольно суровой) из разных разделов алгебры. Сегодня поговорим о профильном ЕГЭ по математике: устойчивые выражения часто встречаются в задании 18, где требуется работать с параметрами.

Вообще, существует два глобальных способа решить задачу с параметром:
1. Графический метод — строим графики и анализируем полученный чертёж;
2. Аналитический метод — упрощаем уравнения и неравенства с помощью алгебраических преобразований.

Графический метод хорош там, где графики легко рисуются: параболы, прямые, окружности, модули. Аналитический метод подключается к делу тогда, когда нарисовать график функции не представляется возможным. И сегодня мы поговорим именно о таких задачах.

00:03 Повторение: что такое устойчивые выражения
02:30 Задание 1: формула квадрата разности
17:39 Выводы по заданию 1
18:48 Задание 2: формула разности квадратов
30:09 Выводы по заданию 2

Предлагаю вашему вниманию действительно сложное и интересное задание 18 из профильного ЕГЭ по математике. Нет, это не просто очередная задача с параметром. Чтобы составить эту задачу, авторы использовали старинный рецепт:
1. Взять уравнение, которое не решается;
2. Добавить к нему дробно-рациональное неравенство, которое не раскладывается на множители;
3. Добавить туда немного параметров — и попросить, чтобы мы их нашли.:)

Вердикт: если бы такое давали в основной волне ЕГЭ, проходные баллы по математике в ведущих университетах сильно подкосились бы. А это значит, что данная задача достойна нашего рассмотрения. Так что вперёд!:)

00:03 Краткая вводная: немного об оценке корней уравнения
04:36 Условие задачи и первый шаг: исследование функции на монотонность
09:45 Оценка единственного корня и выводы из неё
15:17 Разложение на множители левой стороны неравенства
22:32 Выводы и основные идеи, которые мы использовали для решения

Замечательная задача с параметром из моей коллекции. В настоящем ЕГЭ её не было — для задания 18 она считается слишком сложной. В процессе решения мы вспомним столько алгебраических фактов, что хватило бы на две задачи из второй части. И в этом вся её красота.:)

00:05 Краткая вводная: замечание о непрерывных функциях
03:22 Собственно, задача
07:50 Замена переменной
12:58 Определяем количество корней (но не сами корни!)
19:15 То же самое для второго уравнения (обратите внимание на параболу!)
23:38 Сравнение иррациональных чисел
28:14 Заключение: ещё раз про область значения функции

Если в задаче с параметром вам попадётся очень сложное выражение, к которому непонятно как подступиться, то велика вероятность, что нужно выделить точный квадрат или воспользоваться другими формулами сокращённого умножения. При этом, возможно, потребуется временно поменять местами параметр и, собственно, исходную переменную. Но в результате значительно упрощается решение всей задачи.:)

Основная страница урока:
https://www.berdov.com/docs/pa....rametr/tochnie-kvadr

Разбор довольно сложной задачи 18 из ЕГЭ по математике. Рашается она стандартно — с помощью симметрии корней. Однако эту симметрию надо обнаружить в достаточно сложной системе, которая содержит дроби и тригонометрию.

Как строго обосновать свои рассуждения и при этом не перегружать решение чрезмерными выкладками — об этом поговорим в сегодняшнем видео.:)

Основная страница урока:
https://www.berdov.com/ege/par....ametr/prodvinutaya-s

Аналитическое решение задачи 18 с параметром. Применение формул сокращённого умножения и выделение точного квадрата. Очень эффективный алгоритм для решения сложных задач, где нельзя привлечь графические иллюстрации.

Аналитическое решение задачи 18 с параметром. Квадратное уравнение или неравенство с параметром может перестать быть квадратным, если коэффициент при старшем члене обнуляется.
Оригинал урока:
http://www.berdov.com/ege/para....metr/analiticheskiy-

При изучении модулей наибольшие сложности вызывают уравнения, содержащие несколько модулей, вложенных друг в друга. Решать именно такие уравнения мы и будем в сегодняшнем видеоуроке.:)

Оригинал видео:
http://www.berdov.com/docs/mod....uli/uravnenie-modul-

http://www.berdov.com/ege/para....metr/metod-mazhorant
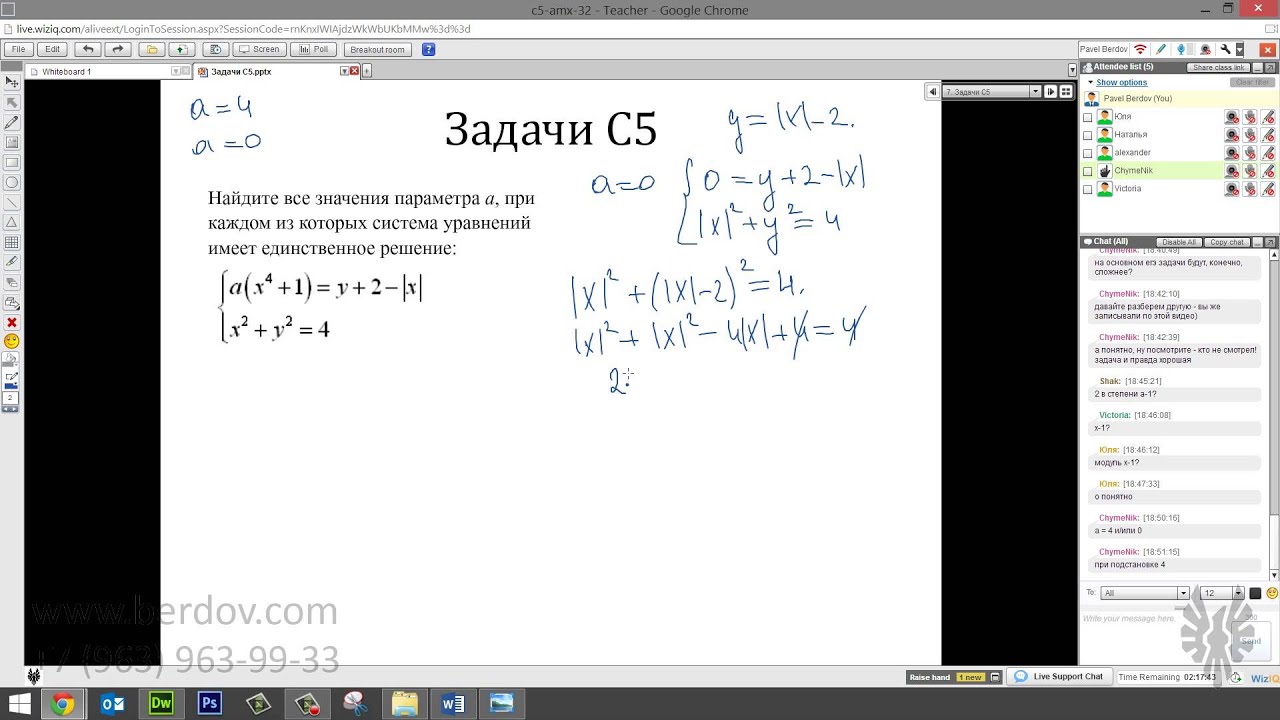
В этом коротком видеоуроке мы рассмотрим сразу два ключевых приема для решения задач C5 из ЕГЭ по математике. Речь пойдет о методе мажорант (ограничение неравенств с целью преобразования их в простые уравнения), а также о методе симметричных корней (банальный, но очень эффективный прием для упрощения систем уравнеинй).

http://www.berdov.com/ege/para....metr/simmetrija-korn
Метод симметричных корней — мощнейший инструмент для решения задачи C5 в ЕГЭ по математике. Однако далеко не всегда эта симметрия видна без предварительных преобразований.
В этом уроке репетитор по математике Павел Бердов разберет именно такую задачу C5, которая решается методом симметрии, однако увидеть эту симметрию — задача отнюдь не тривиальная для неподготовленного ученика.

Математика — это просто. Приходите на занятия и убедитесь в этом сами: http://www.berdov.com
Математика — наука о числовых закономерностях. И если в сложной задаче подметить какую-либо полезную закономерность, то все решение резко упрощается.

Задачи C5 — не исключение. Здесь очень часто требуется начти такие значения параметра A, при которых уравнение имеет ровно один корень. И очень часто получается так, что единственным корнем может быть только X = 0. В противном случае возникают пары противоположных корней, что не удовлетворяет условию задачи.

Поэтому когда вы видите большое и сложное уравнение, к которому ну никак не подступиться, попробуйте симметрию: вдруг корни идут парами? Как убедиться в наличии таких пар — об этом наш сегодняшний урок.

Оригинал:
www.berdov.com/ege/parametr/me....tod-simmetrichnih-ko

Оригинал взят отсюда:
http://www.berdov.com/ege/para....metr/metod-pentagram

Оригинал взят отсюда:
http://www.berdov.com/ege/para....metr/parametr-analit

5:25 — первая задача (попроще);
32:47 — вторая задача (она сложнее, поскольку фигуры там более навороченные).

UPD: 26:30 — ошибочно записано уравнение показательной функции. Там показатель не x - 3,5, а x - 4,5. Из-за этого при графическом решении ответ получился вдвое больше, чем при аналитическом. Правильное значение параметра: a = 1/4.:)

В основу этого видео легли две сложные задачи из ЕГЭ по математике. Однако те приёмы, которые мы сегодня разберём, настолько универсальны и настолько упрощают графическое решение задач с параметром, что их ценность выходит далеко за рамки профильного экзамена.

Оригинал видео:
http://www.berdov.com/docs/par....ametr/rasstoyaniya-n

Не, ну вот это должны знать все. Высота в треугольнике — это просто перпендикуляр из вершины треугольника к противолежащей стороне. При всей очевидности определения у этой самой высоты куча всяких свойств и фишек. О них сегодня и поговорим.:)

13:23 — в условии задачи допущена ошибка: AM = 4, а не 5.:)

Теорема косинусов — более общий приём, нежели теорема Пифагора. Применяется для любого треугольника, в котором известны две стороны и угол между ними, что позволяет найти третью сторону.

Оригинал видео:
http://www.berdov.com/docs/tre....ugolnik/teorema-kosi

Прямоугольные треугольники — особая "каста" в планиметрии. Для них справедлива теорема Пифагора и множество других специальных свойств, которые значительно упрощают и расширяют работу с ними.

Сегодня мы рассмотрим, как возникает подобие прямоугольных треугольников и какие полезные свойства из этого можно извлечь. Оригинал видео:
http://www.berdov.com/docs/tre....ugolnik/podobie-prya

Биссектриса — это луч, который делит угол пополам. В треугольнике биссектрисы обладают важным свойством: они делят противоположную углу сторону на отрезки, пропорциональные двум другим сторонам.

Что это даёт и как это применять — об этом в нашем сегодняшнем видеоуроке. Оригинал видео:
http://www.berdov.com/docs/tre....ugolnik/teorema-o-bi