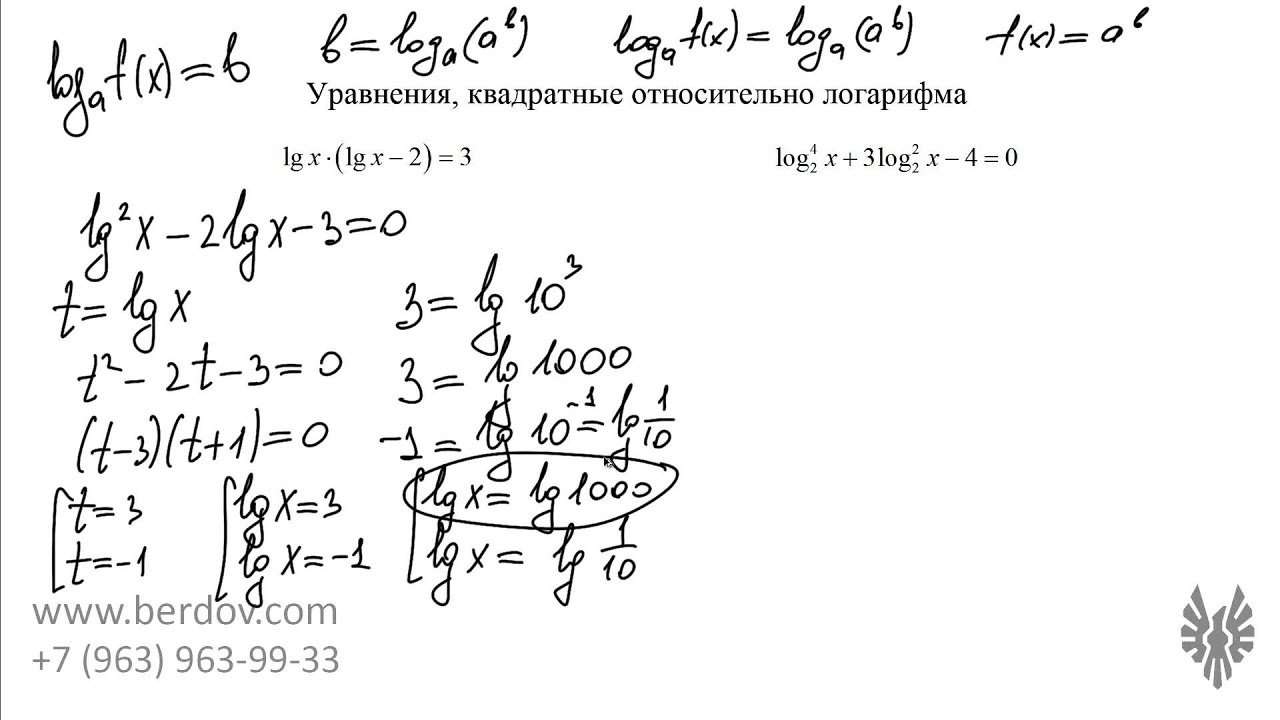http://www.berdov.com/docs/log....arithm/kvadratnie-lo

Еще одна «головная боль» для многих учеников — уравнения, в которых логарифм присутствует во второй и даже четвертой степени. Такие задачи не сводятся к канонической форме и должны решаться через замену переменной.

Любое логарифмическое уравнение решается элементарно, если свести его к канонической форме. Что это за форма и как ее применять — об этом вы узнаете из сегодняшнего видео.

Обзорный урок по основным методам разложения многочлена на множители:
00:03 Обзор основных методов разложения многочленов на множители
14:00 Метод 1: прямое применение распределительного закона
24:58 Замечания по формулам преобразования степеней
26:54 Вспоминаем подобные одночлены и алгебраическую сумму
30:08 Формулы сокращённого умножения: разность квадратов
39:20 Формулы сокращённого умножения: квадрат суммы и разности
48:38 Формулы сокращённого умножения: сумма и разность кубов
53:52 Метод группировки
01:03:47 Комбинированные задачи
01:17:24 Конец :)

Начинаем цикл уроков, посвящённых многочленам и их свойствам. Для успешного освоения этой темы нужно уметь работать со степенями, знать правила их преобразований.

Этот материал относится к 7 классу. Начнём со свойств одночлена, затем будем двигаться к более сложным темам.

Математика — это просто. Приходите на занятия и убедитесь в этом сами: http://www.berdov.com
Бикваюратные уравнения легко сводятся к обычным квадратным с помощью замены переменной, Далее все решается через обычный дискриминант.

http://www.berdov.com/docs/pol....ynom/teorema-bezu-mn

Важнейшим следствием теоремы Безу является то, что корни целочисленного многочлена являются делителями его свободного члена. Этот факт в сочетании с методом деления многочленов уголком позволяет раскладывать на множители такие многочлены, которые иначе были бы просто неприступными.

Математика — это просто. Приходите на занятия и убедитесь в этом сами: http://www.berdov.com
Очень часто при решении алгебраических задач возникает необходимость разделить один многочлен на другой. Классический способ — разложение на множители — зачастую оказывается бесполезен, потому что для этого надо знать корни, а деление многочленов для того и нужно, чтобы эти корни найти.

Но выход есть. Многочлены можно делить друг на друга уголком. Все так же, как с обычными числами, и даже чуть-чуть легче. Смотрите видео и тренируйтесь — это ОЧЕНЬ полезный навык, который неоднократно выручит вас при решении сложных задач, а также на ЕГЭ по математике.:)

Что если в числителе и знаменателе обыкновенной дроби будут стоять не числа, а многочлены? Тогда мы получим рациональную дробь (её ещё называют дробно-рациональным выражением). Подобно обычным дробям, рациональные дроби можно складывать, умножать и сокращать.

Но многочлен — это не число. Тут свои правила. И эти правила намного сложнее, чем для привычных нам чисел. Поэтому сегодня мы решим множество задач с рациональными дробями. Будем складывать и вычитать их, делить и умножать, раскладывать на множители числитель и знаменатель, чтобы затем сократить исходную дробь. В общем, будем делать всё то же самое, что и с обычными дробями, но на более высоком уровне.

00:37 Определение рациональной дроби, её свойства
02:59 Повторяем формулы сокращённого умножения
08:00 Сложение и вычитание рациональных дробей
40:13 Замечание по поводу сокращения рациональных дробей
42:01 Умножение и деление рациональных дробей
00:54 Заключение

Этот урок — не из простых. Но он вполне по зубам среднестатистическому школьнику. А тем, кто готовится к ЕГЭ или ОГЭ, он просто необходим. Попробуйте решить эти задачи самостоятельно, повторите формулы сокращённого умножения и алгоритмы разложения многочленов на множители. Это трудно, нудно, но очень полезно.

В этом коротком видеоуроке вы узнаете, как можно быстро разложить на множители и упростить дробно-рациональное выражение, даже если в нем присутствуют многочлены 3-й или 4-й степени. Автор урока — репетитор по математике в Москве Павел Бердов.

Как грамотно упрощать и сокращать рациональные дроби, зная формулы сокращённого умножения и ещё несколько тонкостей? Как распознать в каждом конкретном выражении ту или иную формулу? Об этом — в сегодняшнем видеоуроке.:)

Оригинал урока:
www.berdov.com/docs/rational/r....acionalnye-vyrazheni

Чтобы научиться выполнять сокращение рациональных дробей, необходимо уметь раскладывать числители и знаменатели на множители (по формулам сокращённого умножения, либо методом группировки), а также выполнять преобразования, связанные со сложением и вычитанием этих самых рациональных дробей.

Оригинал видео:
http://www.berdov.com/docs/rat....ional/sokrashenie-ra

Ссылка на видео про многочлены, упомянутое в уроке:
https://www.youtube.com/watch?v=GXRQ7TcovzQ

Это задание я сконструировал специально для своих учеников на основе довольно интересного неравенства из ДВИ МГУ. Конечно, в первой части настоящего ЕГЭ ничего подобного вы не увидите (особенно в задании 5).

Зато одно это неравенство позволит нам повторить и иррациональные неравенства, и метод интервалов, и даже сравнение иррациональных чисел — камень преткновения многих учеников в заданиях 15, 17 и 19. Поэтому внимательно изучите это задание, а ещё лучше — попробуйте решить самостоятельно.

00:03 Краткая вводная: что, собственно, нам предстоит решать?
04:33 Формулировка задачи и предварительные соображения
09:11 Деление многочлена на многочлен — очень полезный приём
13:35 Сравниваем иррациональные числа
22:30 Решаем основное неравенство
37:30 Ответ к первой части задачи (решили неравенство)
39:35 Поиск наибольшего числителя
50:10 Заключение

Иррациональное неравенство — это любое неравенство, содержащее переменную под корнем. Сегодня мы разберём два важнейших типа таких задач:
1. Корень больше функции;
2. Корень меньше функции.
Знания, которые вы получите на сегодняшнем уроке, покрывают примерно 80% всех подобных задач, которые встречаются на типичных контрольных работах, зачётах и экзаменах.

А как же с остальными 20%? О них мы поговорим в отдельных видео.:)

Когда в неравенстве встречается арифметический корень, многие ученики теряются и не понимают, как решать такую конструкцию. Сегодня мы разберем эффективный прием, позволяющий избавиться от корней в неравенстве и при этом не потерять (но и не добавить) корни.

http://www.berdov.com/docs/ine....quality/kvadratnoe-n

Такие задачи очень часто дают на всевозможных контрольных работах и экзаменах. При всей внешней схожести приведенные два неравенства дают совершенно разный ответ. Будьте внимательны и не допускайте обидных ошибок.

Математика — это просто. Приходите на занятия и убедитесь в этом сами: http://www.berdov.com
В этом уроке мы разберем еще одно иррациональное неравенство. Будьте внимательны: несмотря на кажущуюся простоту, подобные неравенства зачастую становятся источником проблем даже для подготовленных учеников.

А все потому что приходится разбирать сразу ДВЕ СИСТЕМЫ неравенств. В общем, будьте внимательны и не наступайте на чужие грабли.:)

Полная версия урока:
www.berdov.com/docs/inequality..../irrational_radical_

http://www.berdov.com/docs/rad....ikal/irracionalnoe-n

Зачастую ученики чувствуют себя неуверенно, если в неравенстве присутствует слишком много отрицательных слагаемых. Сегодня мы раз и навсегда решим эту проблему, для чего разберем иррациональное неравенство вида «корень больше функции», в котором помимо минусов ничего другого и не будет.:)

http://www.berdov.com/docs/rad....ikal/irracionalnoe-n

В пятом, заключительном видео из серии уроков, посвященных иррациональным неравенствам вида «корень больше функции», мы рассмотрим довольно серьезную задачу, для решения которой нам потребуется вспомнить материалы из других разделов математики.
Во-первых, в этой задаче присутствуют дроби. Поэтому в процессе решения возникнет дробно-рациональное неравенство. А во-вторых, после всех преобразований в числителе возникнет многочлен третьей степени, который нужно разложить на множители. Следовательно, нам придется вспомнить теорему Безу и следствия из нее.

http://www.berdov.com/docs/rad....ikal/irracionalnoe-n

Еще одно иррациональное неравенство вида «корень больше функции». Довольно хитрая задача, в которой многие ученики допускают ошибки.
И даже знание формулы перехода от неравенства к совокупности систем (именно так!) зачастую не спасает нас от обидных вычислительных ошибок. Будьте внимательны!

http://www.berdov.com/docs/rad....ikal/irracionalnoe-n

Продолжаем изучать иррациональные неравенства вида «корень больше функции». В этот раз рассмотрим общую схему решения таких задач, а заодно познакомимся с очень эффективным инструментом для самопроверки — прилеганием корней к разделяющему числу.