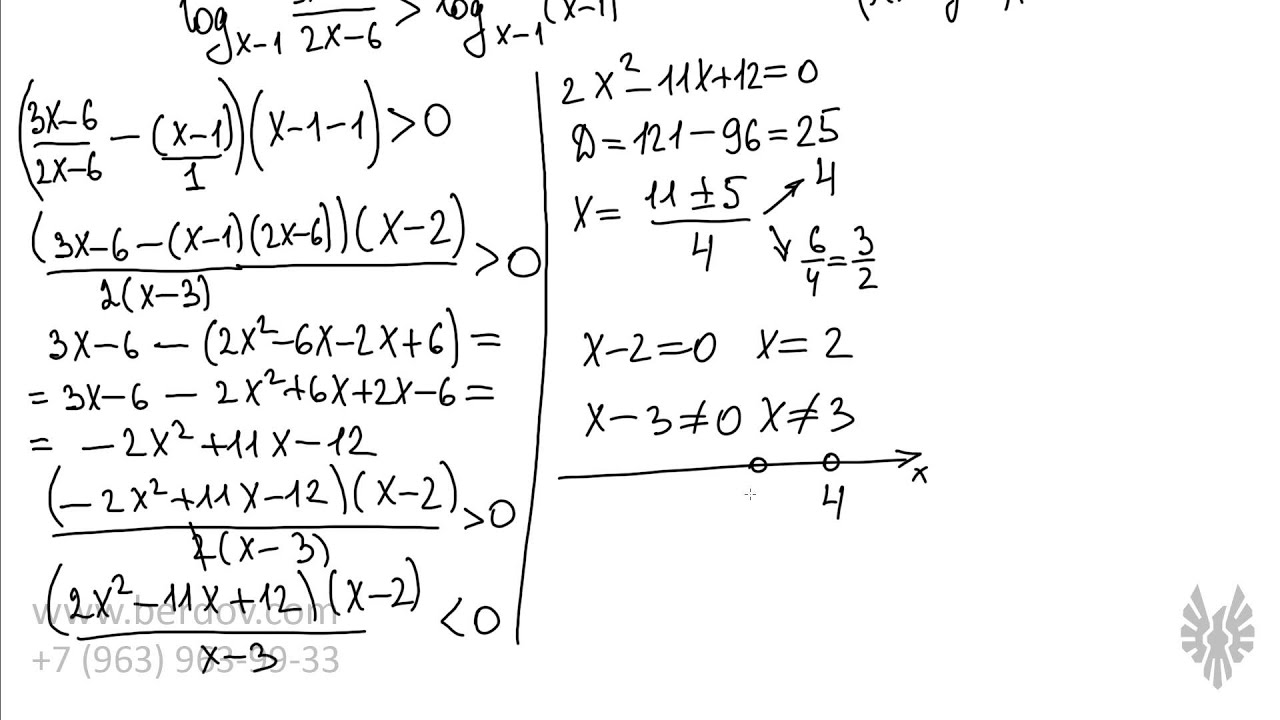При решении логарифмических неравенств нужно внимательно отслеживать область определения логарифмов. Лучше всего ориентироваться на ОДЗ исходного неравенства — так вы гарантированно не потеряете корни и не добавите в ответ ничего лишнего.:)

Решение несложного, но довольно нестандартного логарифмического неравенства, содержащего модуль. Заодно научимся работать с модулем и выносить степени из-под знака логарифма (при условии, что в логарифме находится функция, а не константа).

Решение логарифмического неравенства, содержащего функцию ЗА пределами логарифма. Есть несколько методов работы с такими задачами. Мы рассмотрим наиболее очевидный — внесение множителя в виде степени под знак логарифма.

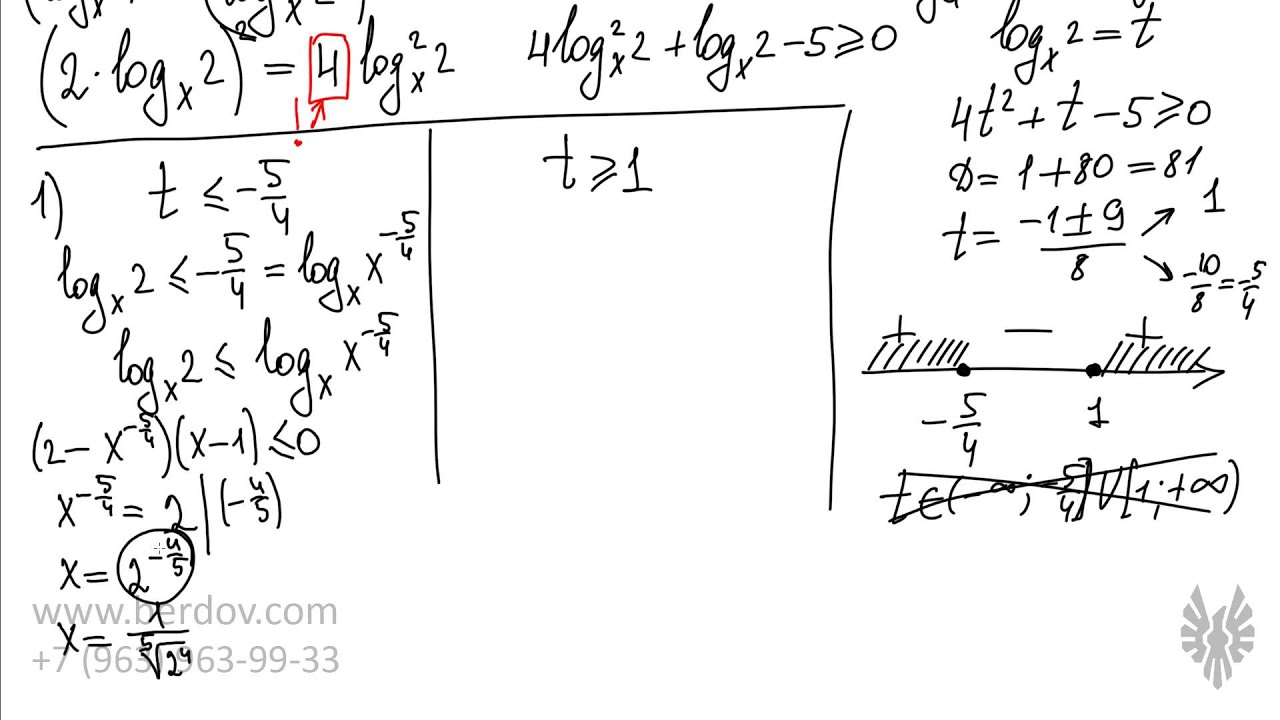
Решение задачи 15 из ЕГЭ по математике. Система из логарифмических и показательных неравенств. Отбор корней и учёт области определения логарифма. Подготовка к профильному ЕГЭ 2016.

0:00 Вступление: основные принципы решения логарифмических неравенств
3:34 Решене задачи 15 с логарифмами из ЕГЭ по математике
22:29 Краткое резюме урока

Оригинал видео:
http://www.berdov.com/ege/sist....ema-neravenstv/logar

Решение логарифмических неравенств методом рационализации. Как вообще можно решать такие неравенства, что делать с переменным основанием логарифма и что такое метод рационализации. Этот урок будет полезен тем, кто изучат логарифмы или серьёзно готовится к ЕГЭ по математике.

0:00 Вступление
0:24 Пример решения логарифмического неравенства с переменным основанием
5:50 Комментарий по поводу сравнения иррациональных чисел и обоснования ответа

Оригинал видео:
http://www.berdov.com/docs/log....arithm/metod-raciona

Логарифм с переменным основанием. В первую очередь рассматриваем логарифмическую функцию для решения неравенств. В большинстве случаев для этого будет очень полезным метод рационализации — именно его мы сейчас и будем обсуждать на примере реального логарифмического неравенства из школьного курса алгебры.

0:00 Вступление. Схема приведения логарифмического неравенства к каноническому виду
1:27 Решение логарифмического неравенства
9:10 Заключение

Оригинал видео:
http://www.berdov.com/docs/log....arithm/logarifm-s-pe

http://www.berdov.com/docs/log....arithm/preobrazovani
Если в неравенстве присутствует более одного логарифма, от них нужно избавиться путем специальных преобразований. Однако все подобные преобразования должны выполняться по четким правилам работы с логарифмами, а также с обязательным учетом области определения.

http://www.berdov.com/docs/log....arithm/neravenstvo-l
Сегодня мы рассмотрим, как решается логарифмическое неравенство, в основании которого стоит не число, а функция. Такие конструкции называются логарифмами с переменным основанием, и для них существуют специальные приемы решения.

http://www.berdov.com/docs/log....arithm/kvadratnoe-lo

Сегодня мы разберем логарифмическое неравенство, которое не сводится просто так к канонической форме. Дело в том, что после преобразований возникает функция, квадратная относительно логарифма. Как решать такие неравенства и как не допустить ошибку — вот об этом и поговорим.

http://www.berdov.com/docs/log....arithm/neravenstvo-k

Существует большой класс логарифмических неравенств, которые не сводятся к канонической форме никакими преобразованиями.
В таком случае к нам на помощь приходит замена переменной, однако этим приемом нужно уметь пользоваться. Потому что основная сложность при введении замены — выявить «устойчивое» выражение, которое и будет заменяться.

http://www.berdov.com/docs/log....arithm/drobno-racion

Этот видеоурок примечателен сразу двумя моментами. Во-первых, мы рассмотрим общую схему преобразования дробно-рациональных выражений, содержащих знак логарифма. А во-вторых — познакомимся с десятичным логарифмом и на его примере попробуем еще лучше разобраться в данной теме.

Учимся грамотно преобразовывать логарифмические уравнения с учётом области определения. Основная цель таких преобразований — выделение устойчивого выражения, которое затем мы обозначим новой переменной.

Решение логарифмического уравнения, в котором необходимо "перевернуть" один из логарифмов, чтобы привести всё к одному основанию.

http://www.berdov.com/docs/exp....onenta/pokazatelnye-

Любые показательные уравнения сводятся к простейшим либо с помощью преобразований, либо заменой переменной. В этом видеоуроке репетитор по математике Павел Бердов на конкретном примере объясняет, как решать показательные уравнения более высокого уровня сложности.

http://www.berdov.com/docs/exp....onenta/pokazatelnye-

В этом коротком видеоуроке мы разберем довольно сложное показательное уравнение, которое изначально содержит в себе логарифмическую функцию. Как не растеряться в процессе решения, как правильно ввести замену переменной и случайно не нарваться на лишние корни — смотрите в видеоуроке.

http://www.berdov.com/docs/log....arithm/logarifmiches

Сегодня мы разберем довольно скользкую тему, касающуюся логарифмических уравнений, а, точнее, касающуюся вынесения степеней из аргументов и оснований логарифмов.

http://www.berdov.com/docs/log....arithm/reshenie-pros

В этом уроке мы еще раз вернемся к основному методу решения логарифмических уравнений — через каноническую форму. Обычно такой подход применяется для решения неравенств, но и в уравнениях он оказывается очень эффективен. Главное — внимательно выполняйте преобразования и не теряйте корни при изменениях области определения.

Математика — это просто. Приходите на занятия и убедитесь в этом сами: http://www.berdov.com
Для решения самых простых логарифмических уравнений вам нужна всего одна формула. Никаких областей определения и сложных преобразований — все решается буквально в пару строчек.

http://www.berdov.com/docs/log....arithm/logarifmiches

Сегодня мы рассмотрим более серьезные логарифмические уравнения. Здесь переменная будет стоять не только в аргументе, но и в основании логарифма. Как решать такие задачи? И как не допустить ошибку? Об этом — наш сегодняшний видеоурок.

http://www.berdov.com/docs/log....arithm/reshenie-loga

Это заключительное видео из серии уроков, посвященных логарифмическим уравнениям. В этот раз на примере двух задач мы еще раз пробежимся по всем ключевым моментам решения. Особое внимание будет уделено области определения логарифма — именно в этом вопросе допускается большинство ошибок и неточностей.