- Разработка
- Бизнес
- ИТ и ПО
- Личностный рост
- Дизайн
- Маркетинг
- Красота
- Фотография и видео
- Здоровье и спорт
- Музыка
- Образование
- Подготовка к экзаменам
- Языки
- Работа на компьютере
- Строительство и ремонт
- Кулинария
- Сельское хозяйство
- Фриланс
- ПДД и вождение
- Игры
- Школьное образование
- Профессиональная ориентация
- Шитье и кожевенное дело
- Рукоделие
- Каменные и столярные работы
- Собеседование
- Рыбалка и охота
- Страны
Теорема о симметрии перпендикулярных прямых
Если две прямые, лежащие в плоскости, перпендикулярны, то при симметрии относительно одной из них вторая прямая переходит сама в себя.
Если две прямые, лежащие в плоскости, перпендикулярны, то при симметрии относительно одной из них вторая прямая переходит сама в себя.
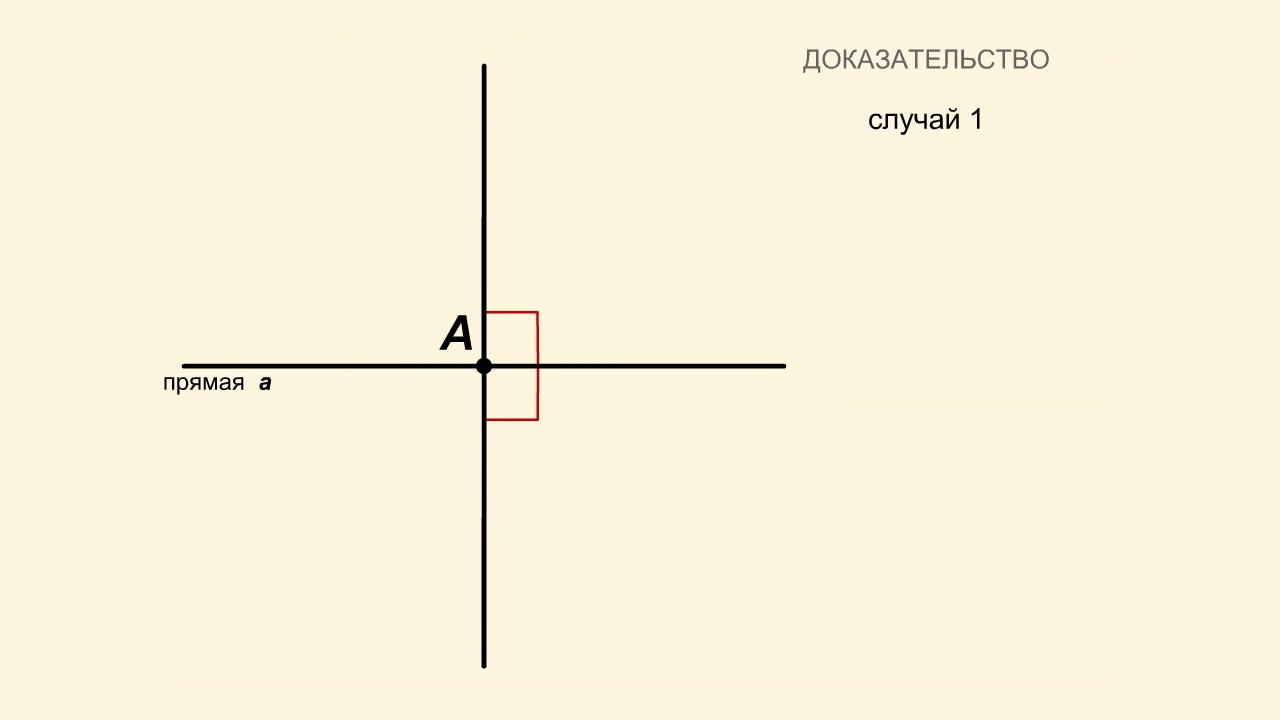
Из определения симметрии следует, что любая фигура при симметрии переходит в равную ей фигуру. Значит, и угол переходит в равный угол. Обозначим рассматриваемые прямые через a и b. Рассмотрим любой из углов, образованных при их пересечении. Сторонами этого угла являются лучи прямых а1 и b1. Этот угол по условию равен 90°.
В результате симметрии относительно a этот угол перейдет в равный ему угол. Но при этом сторона, лежащая на прямой a (луч a1), останется на месте. Значит, другая сторона (луч b1) перейдет в свое продолжение — другой луч той же прямой b (луч b2).