Теорема о диаметре, перпендикулярном хорде
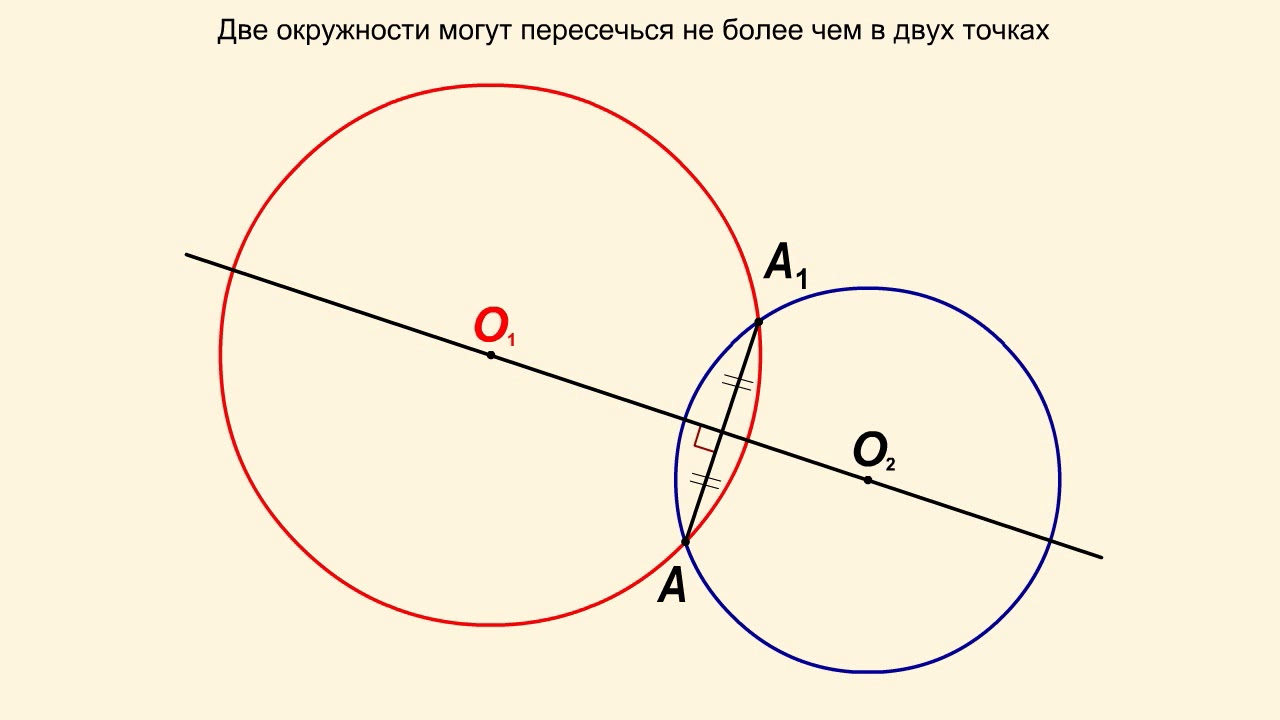
Теорема о равнобедренном треугольнике имеет непосредственное отношение к свойствам окружности. Ведь любую хорду окружности можно рассматривать как основание равнобедренного треугольника, противоположная вершина которого расположена в центре окружности. Этот прием часто используется при доказательстве различных свойств окружности и решении задач.
Свойство хорд окружности можно сформулировать так: «Перпендикуляр, опущенный из центра окружности на хорду этой окружности, делит хорду пополам».
Это же можно выразить несколько иначе: «Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам».
Рассмотрим треугольник OPK, где PK — некоторая хорда окружности, а О — центр.
Этот треугольник равнобедренный: OP = OK. Теперь мы можем воспользоваться свойством равнобедренных треугольников, по которому медиана, биссектриса и высота, проведенные к основанию, совпадают. Значит, перпендикуляр, опущенный из вершины О на PK, делит PK пополам.