Теорема об осях симметрии окружности
Любая прямая, проходящая через центр окружности, является ее осью симметрии.
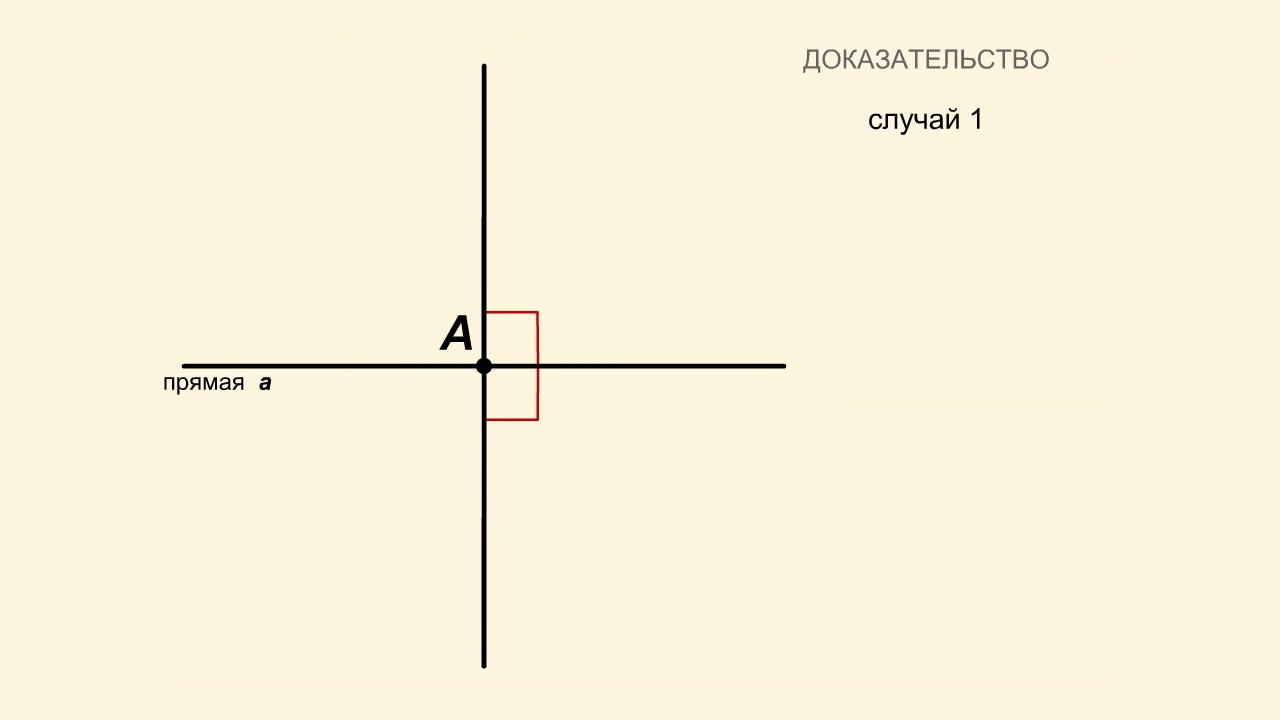
По определению окружность состоит из всех точек плоскости, удаленных на одно и то же расстояние от ее центра. Проведем через центр окружности точку О — произвольную прямую a.
Пусть А — некоторая точка окружности. Если А лежит на прямой а, то в результате симметрии относительно а точка А останется на месте.
Если же А не принадлежит прямой а, то в результате симметрии она перейдет в некоторую точку А', а отрезок ОА — в отрезок OA'. Согласно свойству симметрии
OA = OA',
а значит, и точка А' принадлежит окружности. Но при этой симметрии точка A', в свою очередь, перейдет в А. Короче говоря, при симметрии относительно прямой a точки А и А', лежащие на окружности, просто поменяются местами. Из этого следует, что вся окружность перейдет сама в себя.