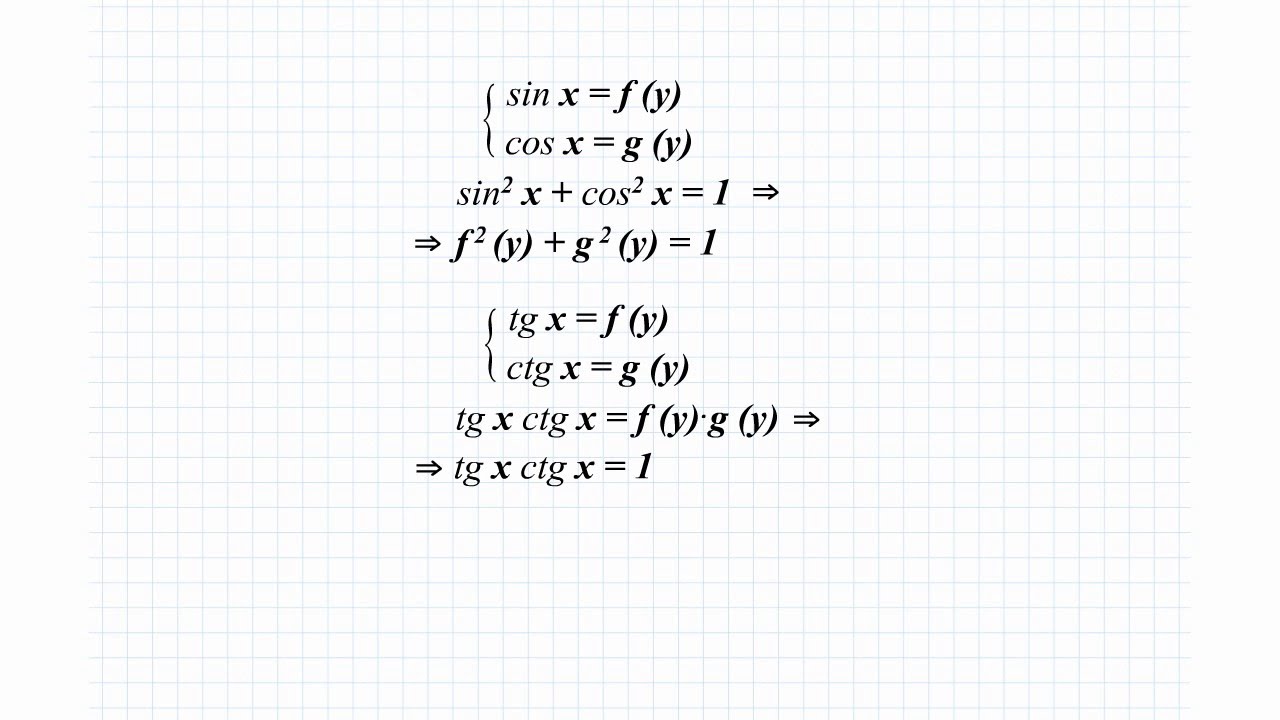Пример из темы " Уравнения и неравенства, содержащие переменную под законом модуля"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Пример из темы " Уравнения и неравенства, содержащие переменную под законом модуля"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Пример из темы " Уравнения и неравенства, содержащие переменную под законом модуля"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Модулем действительного числа х называется само это число, если х положителен, и противоположное число - х, если х отрицателен.

Для решения уравнения или неравенства, содержащего неизвестную величину иод знаком модуля, обычно используют следующий алгоритм:
1) Находим ОДЗ уравнения (неравенства).
2) Найти значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль.
3) ОДЗ уравнения (неравенства) найденными значениями разбивается на промежутки, на каждом из которых выражение, находящееся под знаком модуля, сохраняет знак.
4) Но каждом таком промежутке записать уравнение (неравенство), раскрывая модуль в соответствии со знаком.
5) Решить каждое из полученных алгебраических уравнений (неравенств) на соответствующем промежутке.
6) Объединить решения, найденные на всех промежутках - частях ОДЗ и записать ответ.


Презентации по математике (UA):
https://teachua.com/add/matematyka

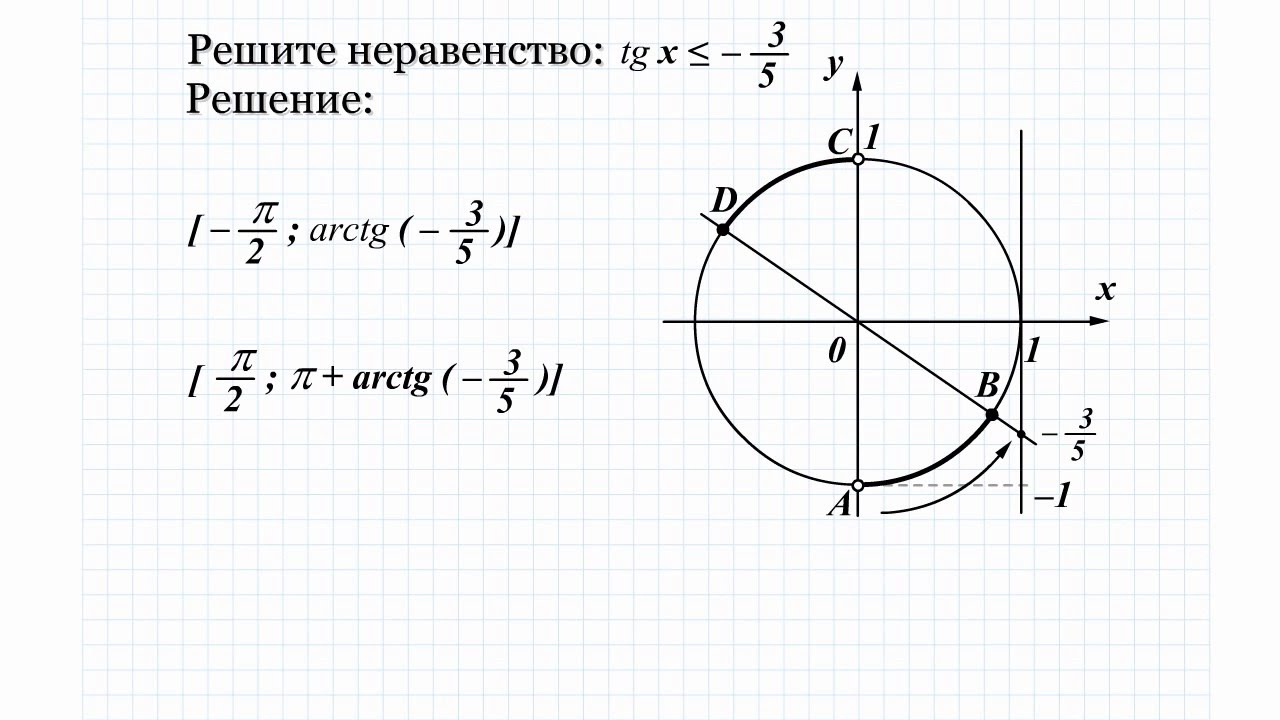
Решение примера из раздела "Решение тригонометрических неравенств"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение задания из раздела "Решение тригонометрических неравенств"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение задания из раздела "Решение тригонометрических неравенств"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение примера из раздела "Решение тригонометрических неравенств"


Презентации по математике (UA):
https://teachua.com/add/matematyka

При решении тригонометрических неравенств необходимо помнить:
1) Свойства неравенств, известные из алгебры;
2) Определение и графики синуса и косинуса;
3) Тригонометрические тождества, уметь выполнять тригонометрические преобразования.


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение системы:
{ sin(x)*cos(y)=0,25
{ sin(y)*cos(x)=0,75


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение системы:
{ sin(x)+cos(y) = 1,5
{ sin^2 (x) + cos^2 (y) = 1,25


Презентации по математике (UA):
https://teachua.com/add/matematyka

При выборе пути тригонометрических систем, следует стараться применять такие преобразования уравнений системы, которые приводят к появлению тригонометрических функций одного аргумента.


Презентации по математике (UA):
https://teachua.com/add/matematyka

краткие видео про для подготовке к экзаменам по физике и математики.


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение уравнения


Презентации по математике (UA):
https://teachua.com/add/matematyka

Метод введения вспомогательного угла

Презентации по математике (UA):
https://teachua.com/add/matematyka

Применение подстановок sin(x)±cos(x)=t

Презентации по математике (UA):
https://teachua.com/add/matematyka

Применение подстановок sin(x)±cos(x)=t

Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение уравнения методом понижения степени


Презентации по математике (UA):
https://teachua.com/add/matematyka

Приведены формулы понижения степени.


Презентации по математике (UA):
https://teachua.com/add/matematyka