Из темы "Решение показательных неравенств"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Неравенства, содержащие переменную в показателе степени, называются показательными.


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение примера из темы "Решение показательных уравнений"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение примера из темы "Решение показательных уравнений"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение примера из темы "Решение показательных уравнений"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Показательными называются уравнения, содержащие переменную в показателе степени.

Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение задание из темы "Свойства степени с рациональным показателем"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение задание из темы "Свойства степени с рациональным показателем"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение задание из темы "Свойства степени с рациональным показателем"


Презентации по математике (UA):
https://teachua.com/add/matematyka

Для любого числа a определена операция возведения в натуральную степень.
Для любого а!=0 определена операция возведения в нулевую и целую отрицательную степень.


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение иррационального уравнения


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение иррационального уравнения


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение иррационального уравнения


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение иррационального уравнения


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение иррационального уравнения


Презентации по математике (UA):
https://teachua.com/add/matematyka

Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.


Презентации по математике (UA):
https://teachua.com/add/matematyka

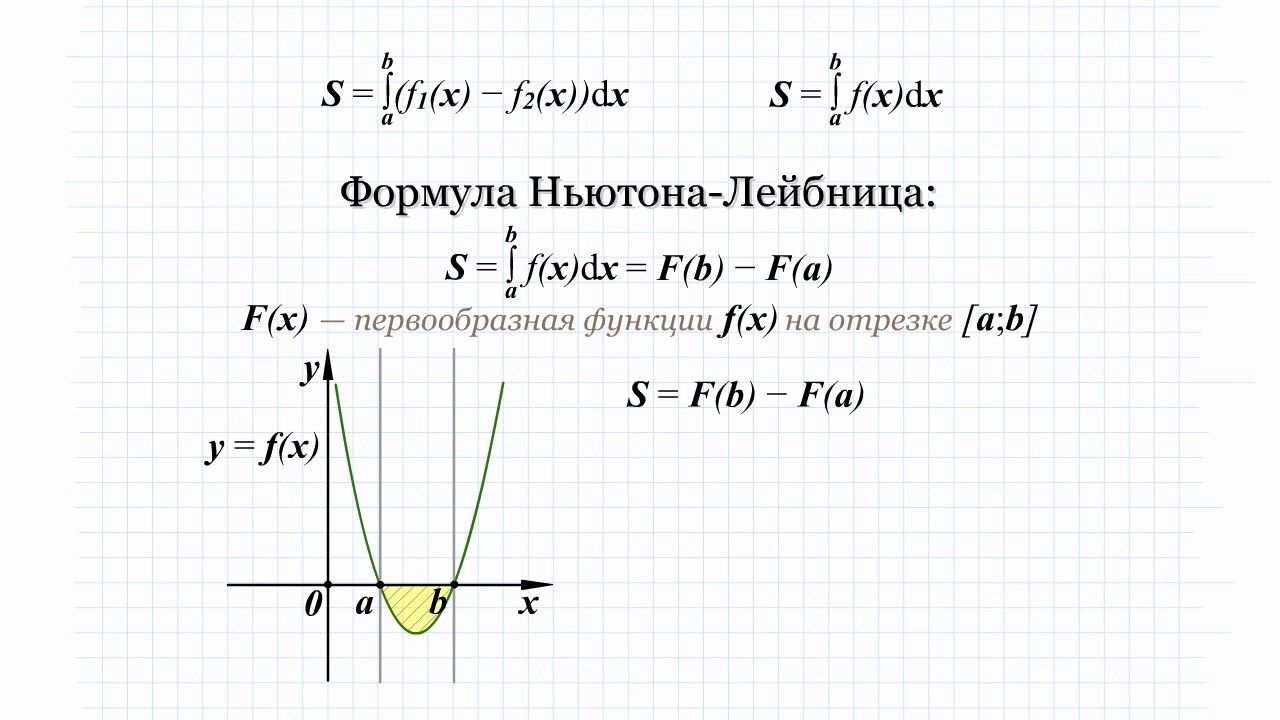
Вычислить площадь фигуры, ограниченной линиями f1(x)=x^2, f2(x)=2x.
Решение задания по математике

Задание: вычислите площадь фигуры, ограниченной линиями.

Решение: построим графики функций y равен x^2 и y равен 2x
Очевидно, что заштрихованная фигура не является криволинейной трапеции
Площадь этой фигуры равна разности площади треугольника OBA и криволинейной трапеции OLBA.
Найдем абсциссы точек пересечения прямой и параболы.
Решая уравнения, получим x1 равен нулю, x2 равен двум.
Таким образом, в принятых обозначениях A равно нулю, B равно двум.
Найдем площадь треугольника как приращение первообразной линейной функции на отрезке от 0 до 2.
Она равна четырем.
Вычислим площадь криволинейной трапеции как приращение первообразной квадратной функции на отрезке от 0 до 2.
Она равна 2 2/3.
Исходя из того, что площадь заштрихованной фигуры равна разности площадей треугольников OBA и криволинейной трапеции OLBA, то окончательно получим площадь фигуры, которая равна 1 1/3.

Презентации по математике (UA):
https://teachua.com/add/matematyka

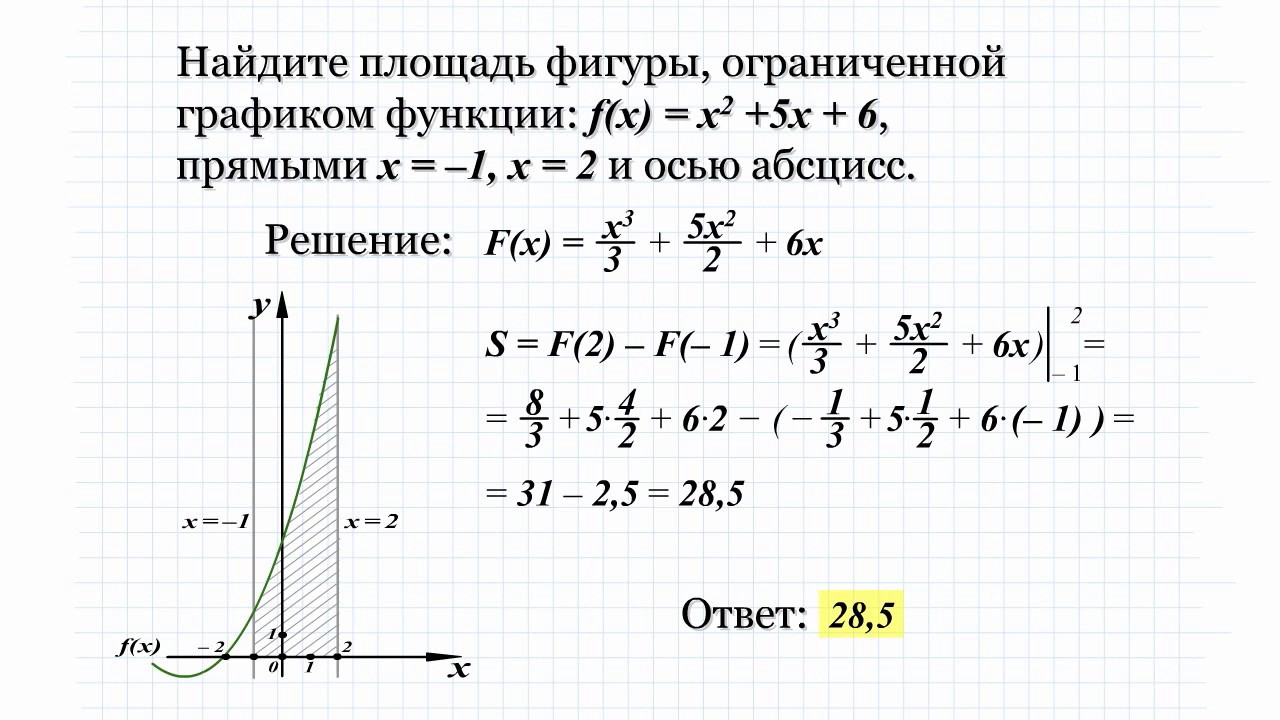
Найдите площадь фигуры, ограниченной графиком функции f(x)=x^2+5x+6, прямыми x=-1, x=2 и осью абсцисс.


Презентации по математике (UA):
https://teachua.com/add/matematyka

Вычисление площади фигуры, ограниченной задаными линиями


Презентации по математике (UA):
https://teachua.com/add/matematyka

Решение


Презентации по математике (UA):
https://teachua.com/add/matematyka