При вычерчивании окружности с помощью циркуля окружность является траекторией движения точки — кончика циркуля.

Сферу можно получить в результате вращения окружности вокруг ее диаметра.

Сферами с общим центром можно заполнить внутренность шара (конечно, надо добавить еще точку — центр шара).

Когда мы при помощи линейки вычерчиваем прямую линию, то как раз получается, что эта прямая вычерчивается движущейся точкой — кончиком карандаша.

Плоскость можно получить при помощи движения прямой линии. Представьте себе лезвие рубанка, выстругивающего доску. Луч вращающегося маяка также может заметать плоскость или же коническую поверхность.

Теперь, перемещая или вращая плоскость, мы можем заполнить все пространство.

Начнем с точки. Можно считать, что точка — это некое место в пространстве, нечто, не имеющее размеров.

При движении точка будет описывать линию — траекторию движения точки.

Будем теперь перемещать в пространстве линию целиком. При этом в процессе движения сама линия может менять форму, деформироваться. Область, заметаемая при таком движении, будет поверхностью.

Все точки тела можно получить, перемещая в пространстве поверхность.

Точка образуется при пересечении двух линий; не имеет размеров. Или, как говорил древнегреческий геометр Евклид, «точка — это то, что не имеет частей».

Как вы помните, линия появляется при пересечении двух поверхностей.

А как образуется точка?

При пересечении двух линий образуется точка.

Возможно, точка пересечения не одна.

В дальнейшем отдельные точки мы обычно будем обозначать заглавными латинскими буквами A, B, C и т.д.

Точка — это то, что не имеет частей и размеров. Как и поверхность, и линия, точка является математической абстракцией. В реальной жизни не существует предметов, не имеющих размеров. Однако всякий маленький по сравнению с окружением предмет мы считаем точкой. Точка — это мельчайшая частица (атом) геометрии.

Любое геометрическое тело, поверхность, линия, любая геомет­рическая фигура состоит из точек, или, как говорят математики, представляет собой множество точек.

Древнегреческий геометр Евклид говорил, что «точка — это то, что не имеет частей». Мы можем добавить, что точка не имеет размеров. Всякий очень маленький по сравнению с рассматриваемым окружением предмет мы считаем точкой.

Точкой является отверстие, оставленное иглой в листе бумаги.

Жук на поверхности Земли.

Город на географической карте.

Или наша планета в Солнечной системе.

В геометрии (и не только в геометрии) прямая линия играет исключительную роль. Луч света представляет собой прямую линию.

Натянутая нить — также прямая.

Свободно падающее тело движется по прямой.

Также по прямой движется тело, на которое не действуют никакие силы. В этом состоит первый закон Ньютона, с которым вы познакомитесь на уроках физики.
За учебником Физика 7 класс Перышкин А. В.

Линия образуется при пересечении двух поверхностей; имеет одно измерение — длину.

Линия может и не быть границий поверхности, главное, что она имет одно измерениие — длину.

При пересечении двух поверхностей получается линия.

Линией обычно является граница поверхности. (Если, конечно, у поверхности есть граница.)

Линия не имеет толщины и ширины. У нее лишь одно измерение — длина. Как и поверхность, линия — понятие абстрактное. В реальной жизни мы часто встречаемся с линиями, точнее, с тем, что удобно считать линией. Предмет или что-то иное, одно измерение которого явно преобладает над другими, мы считаем линией. Например, нить, волос, дорога, разделительная полоса на шоссе, государственная граница и т.п. Мы говорим: «длина волоса», «длина дороги», «20 метров веревки», т.е. ограничиваемся для характеристики предмета лишь одним измерением.

А что получится, если ленту Мёбиуса разрезать вдоль штриховой линии, указанной на рисунке?

Полученная поверхность напоминает лист Мёбиуса, но это не лист Мёбиуса.

В отличие от листа Мёбиуса, у этой поверхности две стороны. Двигаясь вдоль этой поверхности и нигде не переходя через край, нельзя вернуться в ту же точку, но с другой (по отношению к этой точке) стороны.

Эта поверхность называется плоскостью. Именно ее свойства мы и будем в дальнейшем изучать. Плоскость мы представляем себе бесконечной во всех направлениях.

В окружающем нас мире без труда можно найти много примеров плоских поверхностей: поверхность конькобежного катка, оконное стекло, поверхность стола или пола, футбольное поле. Их практически можно рассматривать как плоские поверхности, части плоскости.

Приведем примеры некоторых замечательных поверхностей. Если склеить две противоположные стороны листа бумаги, то получится цилиндр.

Если теперь склеить противоположные стороны цилиндра, то получившаяся поверхность называется тором. Иначе говоря, тор можно получить, склеив (не переворачивая) обе пары противоположных сторон листа бумаги.

А что получится, если склеивать противоположные стороны листа бумаги по-другому?

Поверхность называется листом Мёбиуса. Она названа так по имени открывшего ее (вернее, его) немецкого математика Мёбиуса, жившего в XIX веке. Говорят, что свое открытие он сделал, увидев ленту, которую служанка по оплошности неверно сшила.

Эта поверхность называется бутылкой Клейна. Обратите внимание, что ее на самом деле нельзя склеить (попробуйте убедиться в этом сами).

Эти поверхности обладают на первый взгляд невозможным свойством — у них одна сторона. Оказывается, двигаясь вдоль этих поверхностей и нигде не переходя через край, можно вернуться в ту же точку, но с другой (по отношению к этой точке) стороны.

Поверхность — граница геометрического тела; имеет два измерения — длину и ширину. Однако не всякая поверхность является границей какого-либо тела. Главное здесь то, что поверхность, в отличие от тела, имеет лишь два измерения: длину и ширину.

Всякое геометрическое тело имеет поверхность, представляющую собой границу (оболочку) этого тела.

Поверхность геометрического тела делит все пространство на две части: внутреннюю и внешнюю по отношению к этому телу. Чтобы попасть из любой точки, находящейся внутри тела, во внешнюю область, необходимо пересечь поверхность тела.

Поверхность, ограничивающая шар, называется сферой. У всех других известных нам тел поверхности не имеют специальных названий.

Однако не всякая поверхность является границей какого-либо тела.

Главное здесь то, что поверхность, в отличие от тела, имеет лишь два измерения: длину и ширину. Иными словами, никакое тело, каким бы маленьким оно ни было, нельзя расположить так, чтобы оно целиком принадлежало поверхности.

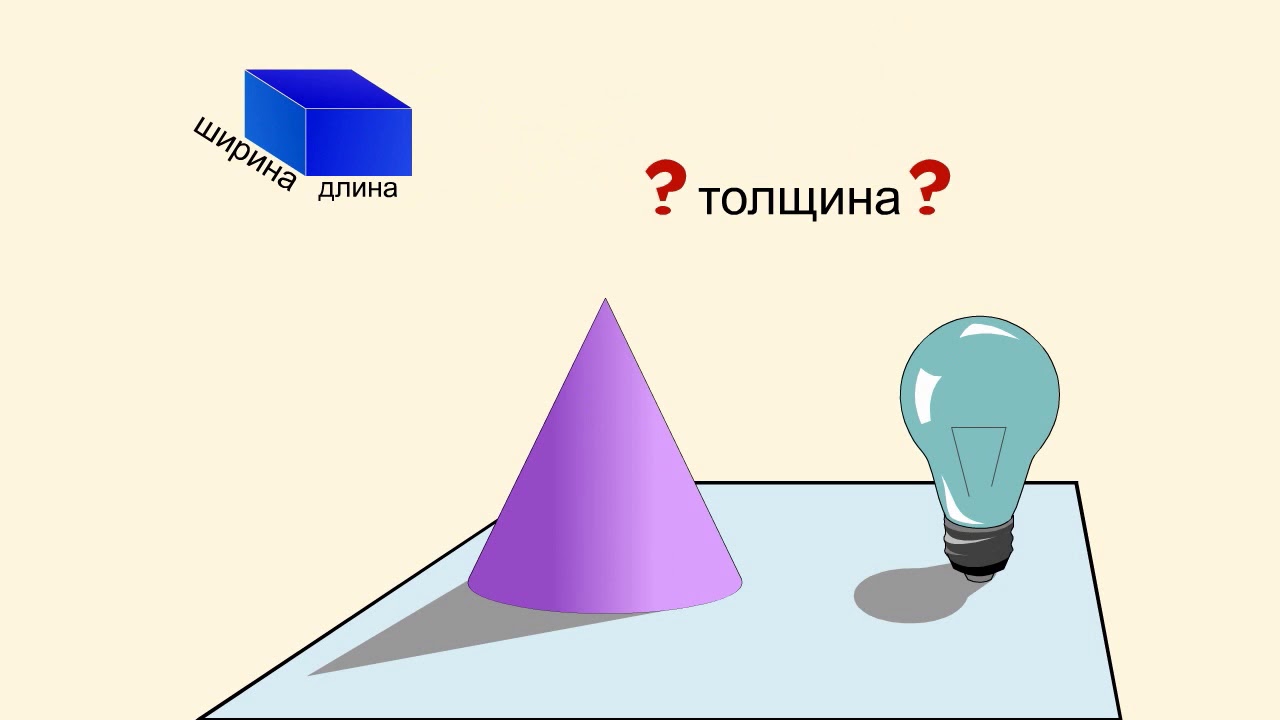
А как быть, допустим, с конусом или каким-то совсем замысловатым телом? Что здесь длина и ширина, а что — толщина?

В общем случае утверждение о наличии у тела трех измерений означает лишь, что внутри него можно поместить параллелепипед, пусть очень небольшой, у которого, однако, все три измерения отличны от нуля.

Можно сказать, что дом и кирпич имеют одинаковую форму — форму параллелепипеда и отличаются только размерами.

Заводская труба имеет форму цилиндра.

Футбольный мяч имеет форму шара.

Конечно, реальный кирпич следует рассматривать как параллелепипед лишь приближенно.

Для практических нужд кирпич удобно рассматривать как параллелепипед.

Важнейшей пространственной формой является геометрическое тело.

Говоря «геометрическое тело», мы тем самым подчеркиваем, что нас не интересуют физические свойства тела: масса, цвет, материал и др., что рассматривать и изучать мы будем лишь его форму и размеры. Можно сказать, что мы рассматриваем ту часть пространства, которую соответствующее тело занимает.

Геометрическое тело — часть пространства; имеет три измерения, которые мы условно называем длиной, шириной и высотой (или толщиной).

Можно сказать, что дом и кирпич имеют одинаковую форму — форму параллелепипеда и отличаются только размерами.

Заводская труба имеет форму цилиндра.

Футбольный мяч имеет форму шара.

Конечно, реальный кирпич следует рассматривать как параллелепипед лишь приближенно.

Для практических нужд кирпич удобно рассматривать как параллелепипед.

Статья об геометрических телах:
https://fizmat.teachua.com/?p=174

Классификация треугольников по сторонам

Свойства равнобедренного треугольника

Перпендикуляр к прямой

Построение равнобедренного треугольника

Первый признак равенства треугольников

Построение угла заданной величины