Последние
Решение иррационального уравнения
Презентации по математике (UA):
https://teachua.com/add/matematyka
Решение иррационального уравнения
Презентации по математике (UA):
https://teachua.com/add/matematyka
Решение иррационального уравнения
Презентации по математике (UA):
https://teachua.com/add/matematyka
Решение иррационального уравнения
Презентации по математике (UA):
https://teachua.com/add/matematyka
Решение иррационального уравнения
Презентации по математике (UA):
https://teachua.com/add/matematyka
Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.
Презентации по математике (UA):
https://teachua.com/add/matematyka
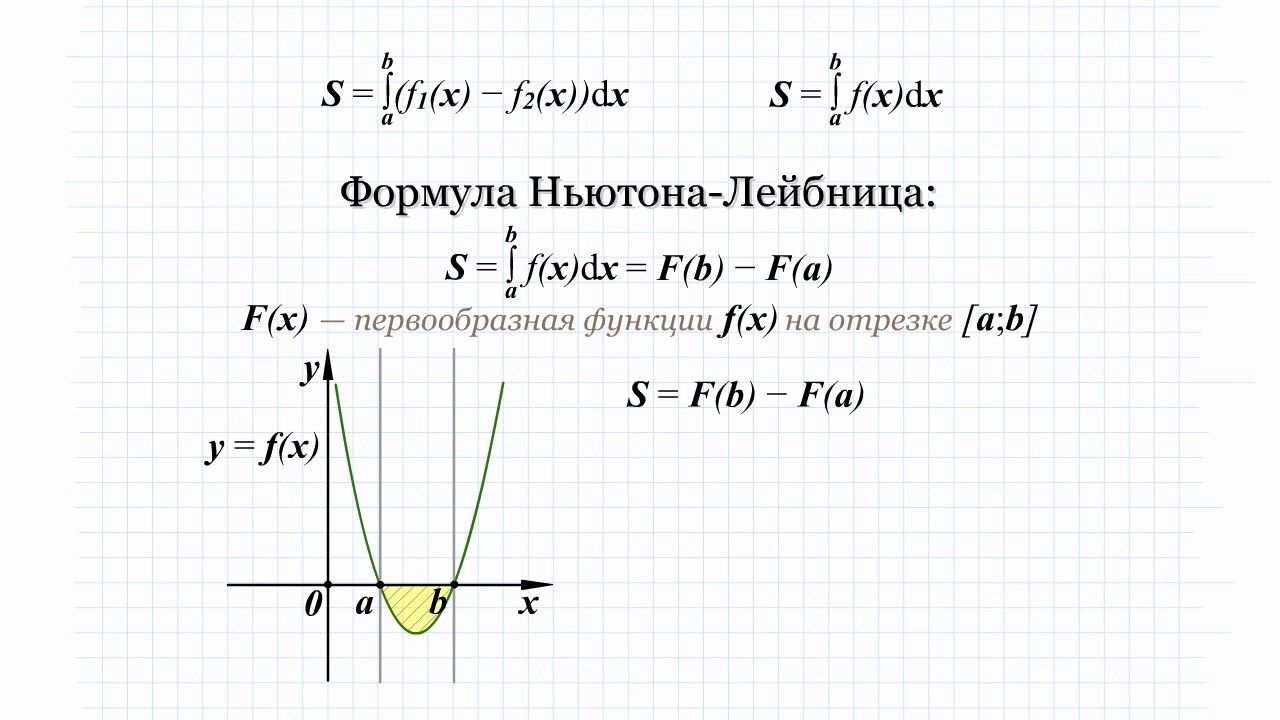
Вычислить площадь фигуры, ограниченной линиями f1(x)=x^2, f2(x)=2x.
Решение задания по математике
Задание: вычислите площадь фигуры, ограниченной линиями.
Решение: построим графики функций y равен x^2 и y равен 2x
Очевидно, что заштрихованная фигура не является криволинейной трапеции
Площадь этой фигуры равна разности площади треугольника OBA и криволинейной трапеции OLBA.
Найдем абсциссы точек пересечения прямой и параболы.
Решая уравнения, получим x1 равен нулю, x2 равен двум.
Таким образом, в принятых обозначениях A равно нулю, B равно двум.
Найдем площадь треугольника как приращение первообразной линейной функции на отрезке от 0 до 2.
Она равна четырем.
Вычислим площадь криволинейной трапеции как приращение первообразной квадратной функции на отрезке от 0 до 2.
Она равна 2 2/3.
Исходя из того, что площадь заштрихованной фигуры равна разности площадей треугольников OBA и криволинейной трапеции OLBA, то окончательно получим площадь фигуры, которая равна 1 1/3.
Презентации по математике (UA):
https://teachua.com/add/matematyka
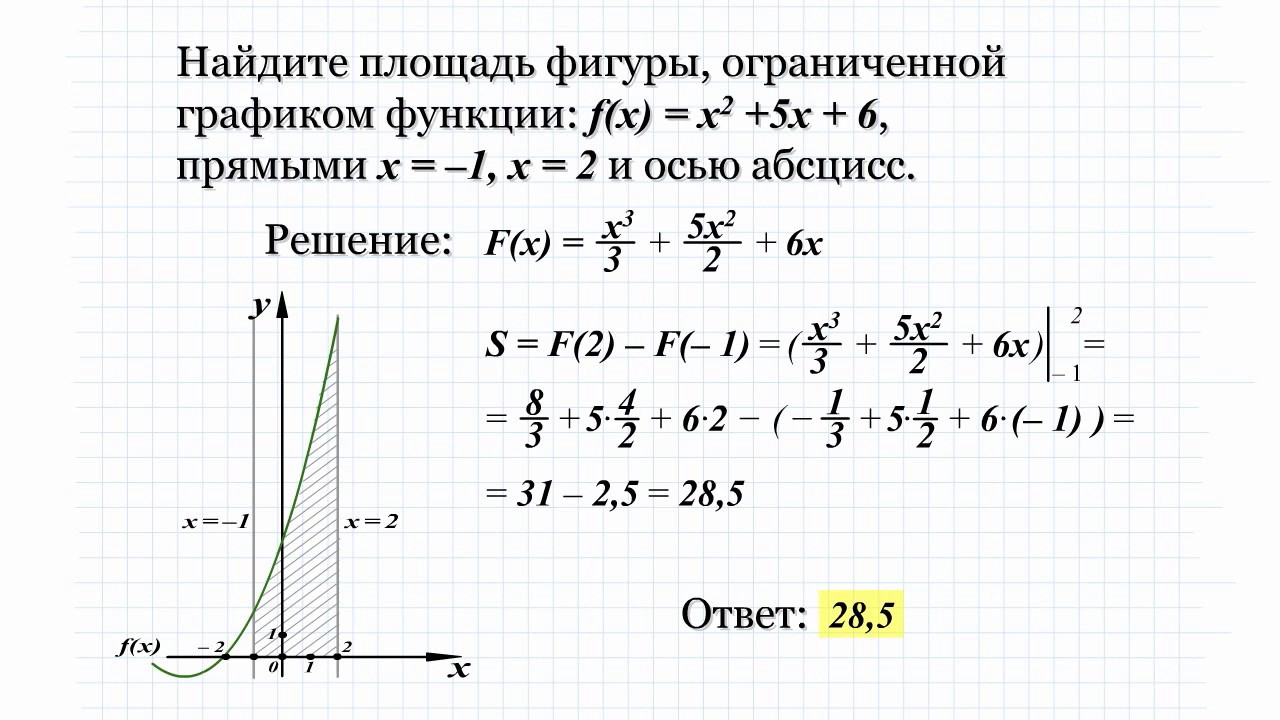
Найдите площадь фигуры, ограниченной графиком функции f(x)=x^2+5x+6, прямыми x=-1, x=2 и осью абсцисс.
Презентации по математике (UA):
https://teachua.com/add/matematyka
Вычисление площади фигуры, ограниченной задаными линиями
Презентации по математике (UA):
https://teachua.com/add/matematyka
Решение
Презентации по математике (UA):
https://teachua.com/add/matematyka
Презентации по математике (UA):
https://teachua.com/add/matematyka
Решение
Презентации по математике (UA):
https://teachua.com/add/matematyka
Презентации по математике (UA):
https://teachua.com/add/matematyka
Найдите среди всевозможных прямоугольных параллелепипедов, у которых одна из базовых граней является квадратом, а периметр нижнего основания равен 12 см, параллелепипед с наибольшим объёмом и вычислите этот объём.
Презентации по математике (UA):
https://teachua.com/add/matematyka
Задача на экстремум — это задача на поиск наибольших или наименьших значений величин.
Представлен алгоритм.
Презентации по математике (UA):
https://teachua.com/add/matematyka
Функция, непрерывная на отрезке, достигает на нем своего наименьшего и наибольшего значений.
1 fx.
2 Найти точки, в которых fх=0 или fх не существует. Отображать те из них, которые лежат внутри отрезка [а;b]
3 Вычислить значения функции у=fх в полученных точках и на концах отрезка, выбрать из них наибольшее и наименьшее: у_наиб., y_наим.
Презентации по математике (UA):
https://teachua.com/add/matematyka
y=2x^3+9x^2-24x
Презентации по математике (UA):
https://teachua.com/add/matematyka
Функция fх называется возрастающей на промежутке I, если для любых x1 и x2 из этого промежутка выполняется неравенство...
Алгоритм исследования функции на промежутки монотонности.
Презентации по математике (UA):
https://teachua.com/add/matematyka
Найти точки экстремума функции f(x)= 2x^3-3x^2-1
Подготовка к экзамену по математике
Презентации по математике (UA):
https://teachua.com/add/matematyka
#математика #экстремум #решение #урок #точки #функции
Тело движется по прямой так, что расстояние S от него до некоторой точки А этой прямой изменяется по закону S = t^3 - 3t + 4, где t - время движения в секундах. Найдите скорость тела через 3 секунды после начала движения.
Презентации по математике (UA):
https://teachua.com/add/matematyka