Теорема о единственности перпендикуляра
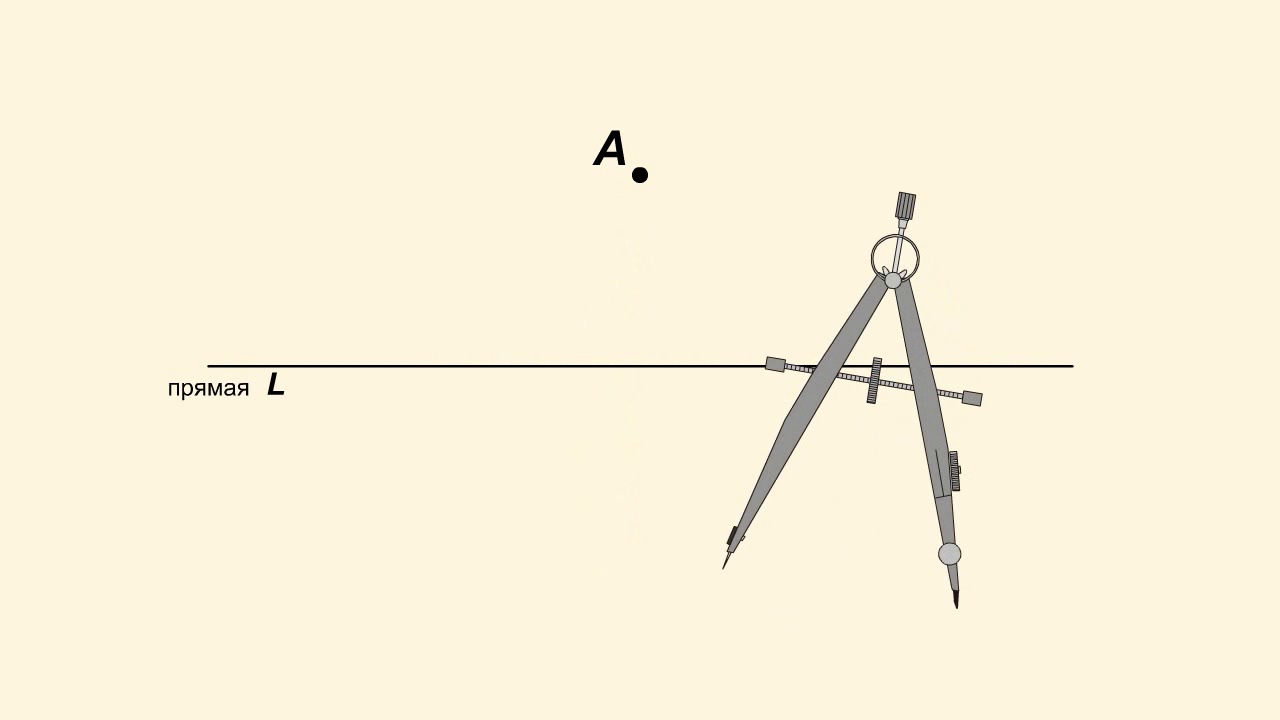
Через любую точку плоскости проходит единственная прямая, перпендикулярная данной прямой.
Пусть точка А лежит на прямой а.
В каждой из двух полуплоскостей, соответствующих прямой а, существует лишь один луч, образующий прямые углы с обеими полупрямыми, на которые точка А разбивает прямую а. Эти два луча лежат на одной прямой, перпендикулярной прямой а.
Рассмотрим теперь случай, когда точка А расположена вне прямой.
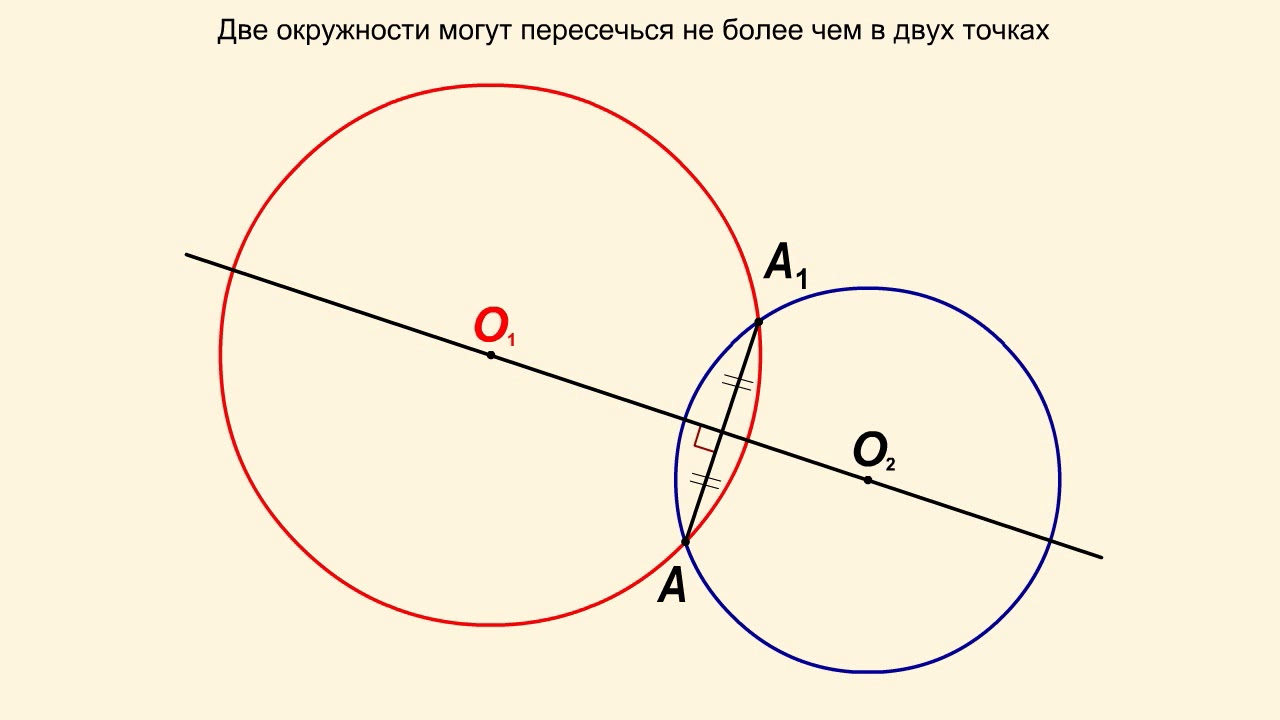
Обозначим через А' точку, симметричную А относительно а. Как мы уже знаем из теоремы о симметрии перпендикулярных прямых, прямая, перпендикулярная а, в результате симметрии относительно а переходит сама в себя. Это означает, что если она проходила через А, то должна проходить и через А'. Следовательно, эта прямая является единственной.