Задания 15 и 16 ЕГЭ по математике (профильный уровень)
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВК: https://vk.com/volkovvalery

Задача 16 из реального ЕГЭ по математике (профиль)
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO = KO.
б) Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/100 площади трапеции ABCD.

Задания № 4, 8, 13, 14, 15, 16 ЕГЭ 2017 (профиль)
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery

ЕГЭ по математике. Профильный уровень. Задача 16.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Тренировочный вариант №121 Александра Ларина. В прямоугольный треугольник АВС вписана окружность, которая касается гипотенузы АВ в точке К, а катетов – в точках Р и М. а) Докажите, что площадь треугольника АВС равна АК∙ВК. б) Найдите площадь треугольника РКМ, если известно, что АК=12, ВК=5.

Задача №16 ЕГЭ по математике профильный уровень.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны АВ и AD в точках M и N соответственно. а) Докажите, что периметр треугольника AMN равен стороне квадрата. б) Прямая MN пересекает прямую CD в точке Р. В каком отношении делит сторону ВС прямая, проходящая через точку Р и центр окружности, если АМ:МВ=1:2?

Задача 16 ЕГЭ по математике. Урок 10.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Окружность с центром O, вписанная в треугольник ABC, касается его сторон AB, AC и BC в точках C1, B1, и A1 соответственно. Биссектриса угла A пересекает эту окружность в точке Q, лежащей внутри треугольника AB1C1. А) Докажите, что C1Q – биссектриса угла AC1B1. Б) Найдите расстояние от точки O до центра окружности, вписанной в треугольник AB1C1, если известно, что BC=7, AB=15, AC=20.

Задача 16 ЕГЭ по математике. Урок 9.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
В треугольнике ABC известно, что угол ∠BAC=60 градусов, угол ∠ABC=45 градусов. Продолжения высот треугольника ABC пересекают описанную около него окружность в точках M, N, P. а) Докажите, что треугольник MNP прямоугольный. б) Найдите площадь треугольника MNP, если известно, что BC=6.

Задача 16 ЕГЭ по математике. Урок 8.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
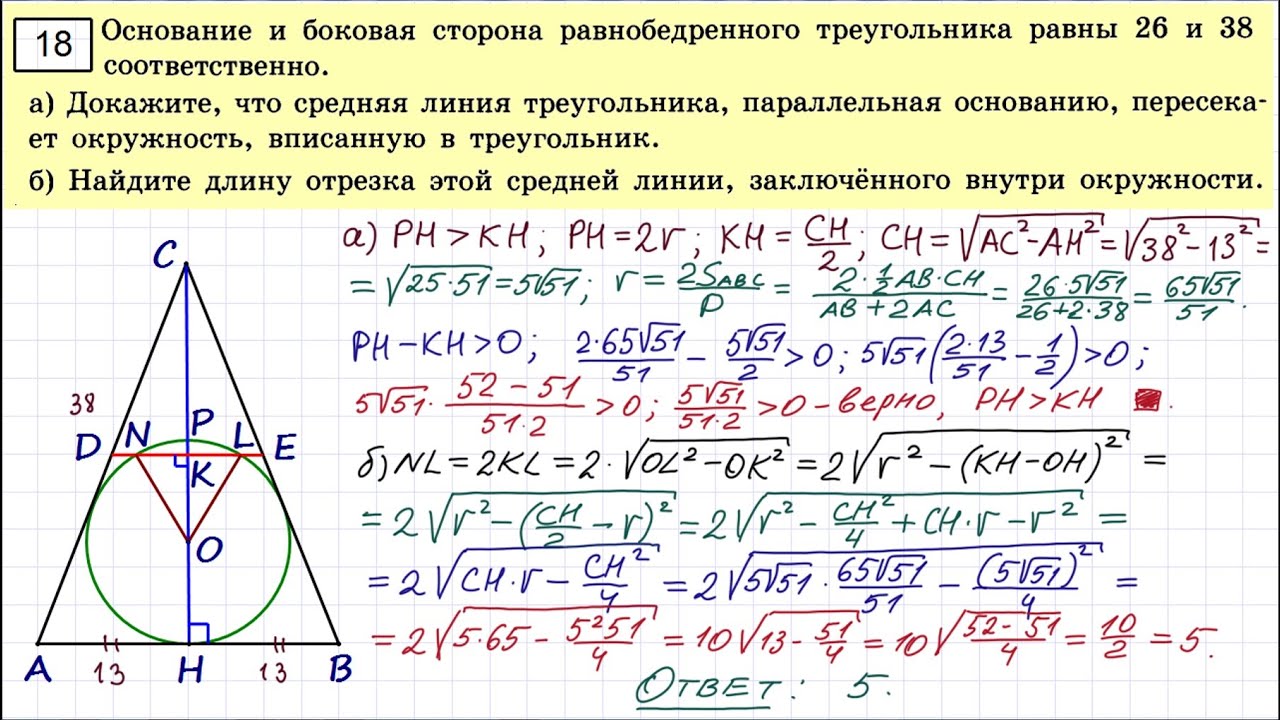
Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно. а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник. б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.

Задача 16 ЕГЭ по математике. Урок 7.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
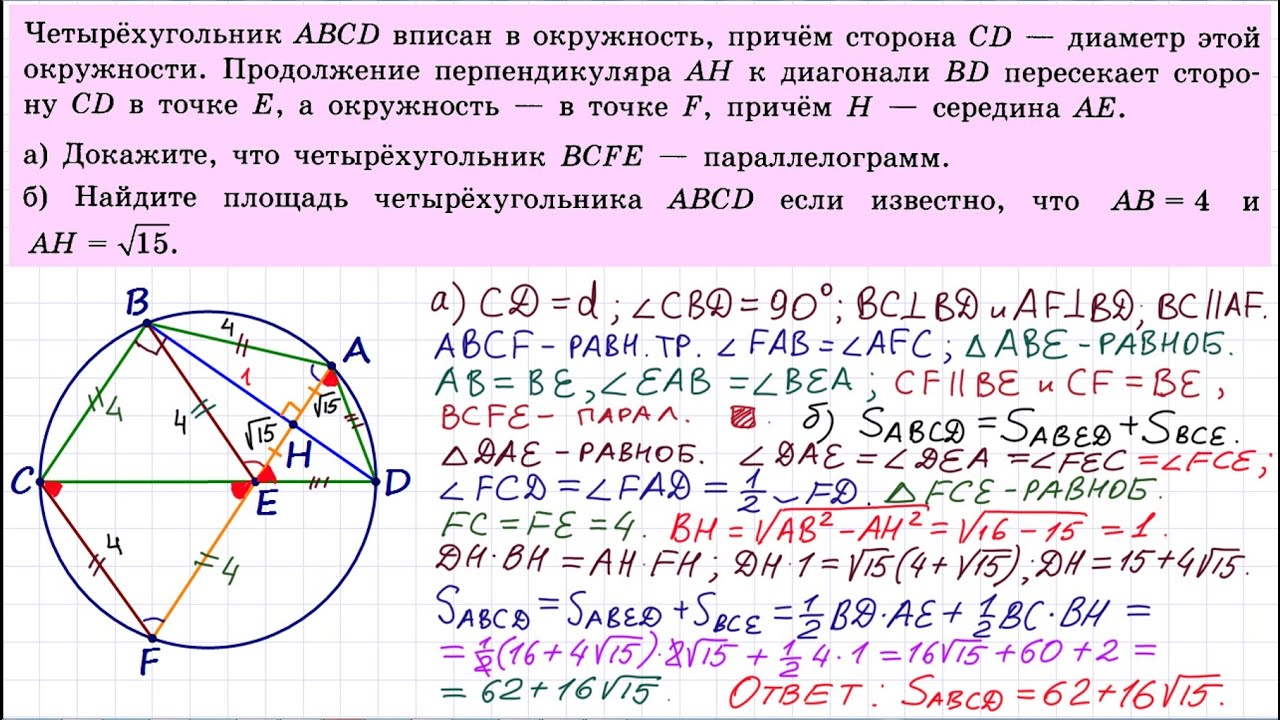
Четырёхугольник ABCD вписан в окружность, причём сторона CD - диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность - в точке F, причём H - середина AE. а) Докажите, что четырёхугольник BCFE - параллелограмм. б) Найдите площадь четырёхугольника ABCD, если известно, что AB=4 и AH=sqrt(15).

Задача 16 ЕГЭ по математике. Урок 6.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Вневписанная окружность равнобедренного треугольника касается его боковой стороны. а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание. б) Известно, что радиус этой окружности в четыре раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

Задача 16 ЕГЭ по математике. Урок 5.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Прямая, параллельная основаниям BC и AD трапеции ABCD, пересекает боковые стороны AB и CD в точках M и N. Диагонали AC и BD пересекаются в точке O. Прямая MN пересекает стороны OA и OD треугольника AOD в точках K и L соответственно. а) Докажите, что MK=NL. б) Найдите MN, если известно, что BC=10, AD=18 и MK:KL=1:2.

Задача 16 ЕГЭ по математике. Урок 4.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30 градусов. Точка E лежит вне прямоугольника, причём ∠BEC=120 градусов. а) Докажите, что ∠CBE = ∠COE. б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE=21 и CE=24.

Демонстрационный вариант ЕГЭ по математике. Задание №16.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C. а) Докажите, что прямые AD и BC параллельны.б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Задание 16. Урок 1.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Медианы АА1, ВВ1 и СС1 треугольника АВС пересекаются в точке М. Известно, что АВ = 3МС. а) Докажите, что треугольник АВС прямоугольный. б) Найдите длину отрезка DN, где D - точка касания стороны АС и вписанной в треугольник АВС окружности, N - точка касания стороны АС и окружности, касающейся стороны АС и продолжений сторон ВА и ВС треугольника АВС, если известно, что АС = 6, ВС = 8.

Задание №16 (бывшее задание №18, С4) ЕГЭ по математике.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
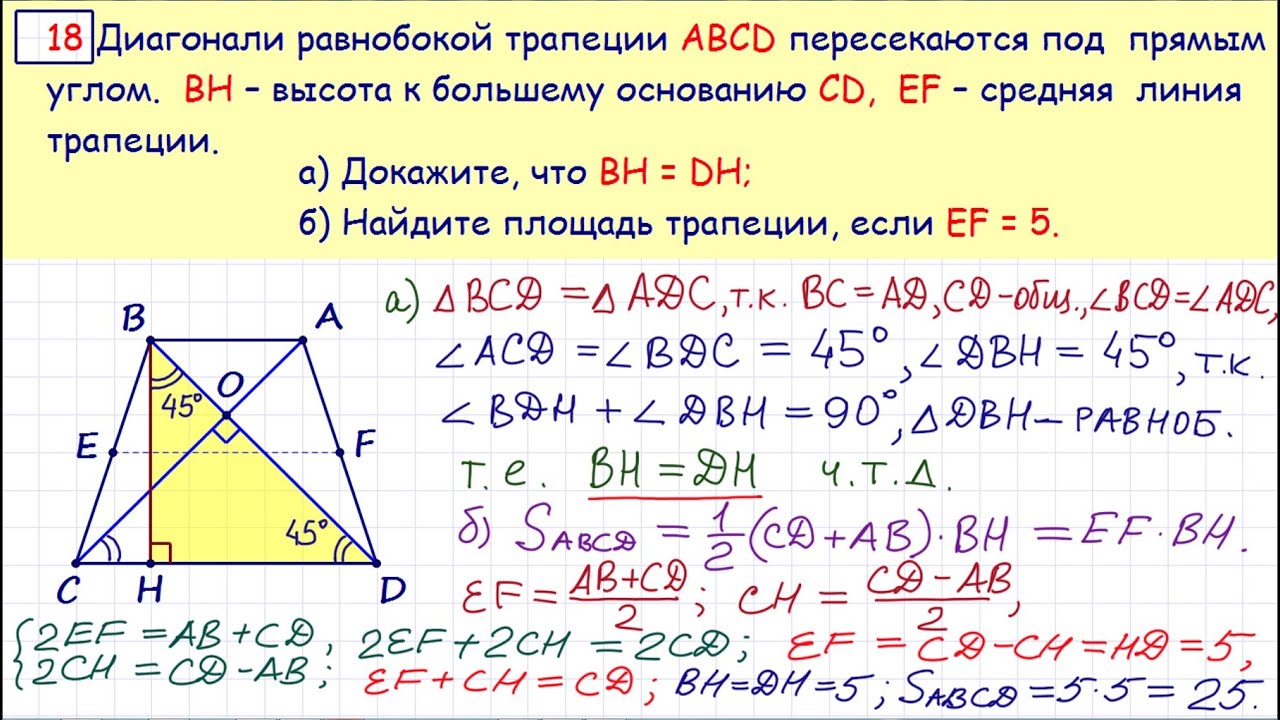
Профильный уровень. Тренировочный вариант №81 Александра Ларина. Диагонали равнобокой трапеции ABCD пересекаются под прямым углом. BH высота к большему основанию CD, EF – средняя линия трапеции. а) Докажите, что BH = DH; б) Найдите площадь трапеции, если EF = 5.

Задание 16 ЕГЭ по математике (профиль).
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая - боковых сторон, меньшего основания BC и первой окружности. а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что AP/PD=sinD. б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

ЕГЭ по математике профильный уровень. Задание 16.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Мои занятия в Скайпе: https://vk.com/id224349278
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Точка О – центр окружности, описанной около остроугольного треугольника АВС, I ‐ центр вписанной в него окружности, H ‐ точка пересечения высот. Известно, что ∠BAC=∠OBC+∠OCB. а) Докажите, что точка I лежит на окружности, описанной около треугольника BOC. б) Найдите ∠OIH, если ∠ABC=55.

Задача с параметром.
Индивидуальные занятия по Скайпу для школьников, студентов, учителей, репетиторов. ЕГЭ, ОГЭ, высшая математика. Начальный уровень значения не имеет.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Почта: uroki64@mail.ru
Видеорешебник задач здесь:
https://vk.com/doc224349278_515790622?hash=329214e6f24e9ae2ec&dl=14177fa26be822e471

Сто тренировочных задач абитуриента #45.
Задание для поступающих в вузы.
Индивидуальные занятия по Скайпу для школьников, студентов, учителей, репетиторов. ЕГЭ, ОГЭ, высшая математика. Начальный уровень значения не имеет.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Почта: uroki64@mail.ru
При каких значениях параметра a уравнение ax^6=e^x имеет одно положительное решение?

Решаем задачи с параметрами.
Индивидуальные занятия по Скайпу для школьников, студентов, учителей, репетиторов. ЕГЭ, ОГЭ, высшая математика. Начальный уровень значения не имеет.
Поддержать Проект: http://donationalerts.ru/r/valeryvolkov
Новая Группа ВКонтакте: https://vk.com/volkovvalery
Почта: uroki64@mail.ru