В данном видеоуроке мы рассмотрим пример решения задачи о раскрое рулонов ткани на куски заданной длины, при котором количество раскроенных рулонов будут минимальным.
Задача будет решаться с помощью Поиска решений Excel.
В заключении будет приведена экономико-математическая постановка данной задачи линейного программирования.

По ссылке https://drive.google.com/open?....id=1xjC6C46TLHnbX_2q можно скачать получившийся в процессе решения задачи файл Microsoft Excel.

Как и обещал в ходе изложения материала, ссылка на первый видеоурок из серии задач о раскрое материалов: https://youtu.be/F3rbR4-q68c

В нашей подборке вы также можете найти больше видеоуроков по решению прикладных задач в Excel https://goo.gl/9LrQZG
Больше других обучающих видеоуроков вы сможете найти на нашем сайте http://goo.gl/kkSWEU

Рассмотрим на практике решение задачи о максимальном потоке в сети с помощью теории графов. В качестве алгоритма решения используем широко известный алгоритм Форда-Фалкерсона.

Таймкоды содержания:
00:17 Вступление
00:45 Экономический смысл задачи о максимальном потоке в сети
01:37 Основные понятия и определения теории графов
02:57 Алгоритм Форда-Фалкерсона
04:19 Пример решения задачи о максимальном потоке в сети

Общий случай с несколькими истоками и стоками рассматривается здесь:
https://youtu.be/F0O1J92aN2k

В нашей подборке вы сможете найти больше видеоуроков по Прикладным задачам в экономике:
http://bit.ly/2VzR1Ik

Еще больше других обучающих видеоуроков вы сможете найти на нашем сайте: http://videolections.blogspot.com/

По вопросам сотрудничества - marcellidenumana@gmail.com

ПОДПИШИСЬ НА КАНАЛ - https://www.youtube.com/c/StudyProf

Буду благодарен за поддержку канала для улучшения контента!
Номер карты (грн.): 5375 4141 1409 0185
Номер карты (usd): 4731 1856 1771 3067

Мой Twitter - https://twitter.com/StudyProf_
Мой Instagram - https://www.instagram.com/study_prof/
Мой FB - https://www.facebook.com/StudyProf/

В прошлом видеоуроке мы с вами уже рассмотрели решение задачи о максимальном потоке с использованием теории графов: https://youtu.be/GxAUU_oQ8fE

Однако, рассмотренный пример предполагал, что у нас имеется ровно 1 исток и 1 сток. И это было необходимым условием для применения алгоритма Форда-Фалкерсона в ее решении.

А сейчас мы рассмотрим общий случай, когда количество истоков или стоков может быть больше одного.

В нашей подборке вы сможете найти больше видеоуроков по Прикладным задачам в экономике:
http://bit.ly/2VzR1Ik

Еще больше других обучающих видеоуроков вы сможете найти на нашем сайте: http://videolections.blogspot.com/

По вопросам сотрудничества - marcellidenumana@gmail.com

ПОДПИШИСЬ НА КАНАЛ - https://www.youtube.com/c/StudyProf

Буду благодарен за поддержку канала для улучшения контента!
Номер карты (грн.): 5375 4141 1409 0185
Номер карты (usd): 4731 1856 1771 3067

Мой Twitter - https://twitter.com/StudyProf_
Мой Instagram - https://www.instagram.com/study_prof/
Мой FB - https://www.facebook.com/StudyProf/

В прошлом видеоуроке мы с вами уже рассмотрели решение задачи о максимальном потоке с использованием теории графов: https://youtu.be/GxAUU_oQ8fE

Однако, рассмотренный пример предполагал, что у нас имеется ровно 1 исток и 1 сток. И это было необходимым условием для применения алгоритма Форда-Фалкерсона в ее решении.

А сейчас мы рассмотрим общий случай, когда количество истоков или стоков может быть больше одного.

В нашей подборке вы сможете найти больше видеоуроков по Прикладным задачам в экономике:
http://bit.ly/2VzR1Ik

Еще больше других обучающих видеоуроков вы сможете найти на нашем сайте: http://videolections.blogspot.com/

По вопросам сотрудничества - marcellidenumana@gmail.com

ПОДПИШИСЬ НА КАНАЛ - https://www.youtube.com/c/StudyProf

Буду благодарен за поддержку канала для улучшения контента!
Номер карты (грн.): 5375 4141 1409 0185
Номер карты (usd): 4731 1856 1771 3067

Мой Twitter - https://twitter.com/StudyProf_
Мой Instagram - https://www.instagram.com/study_prof/
Мой FB - https://www.facebook.com/StudyProf/

В одном из предыдущих видеоуроков мы с вами учились решать транспортные задачи закрытого типа. И в тот раз я сделал замечание, что задача закрытого типа - это всего лишь частный случай транспортных задач. О том, что такое транспортная задача открытого типа и как ее решать, вы узнаете из нашего видеоурока

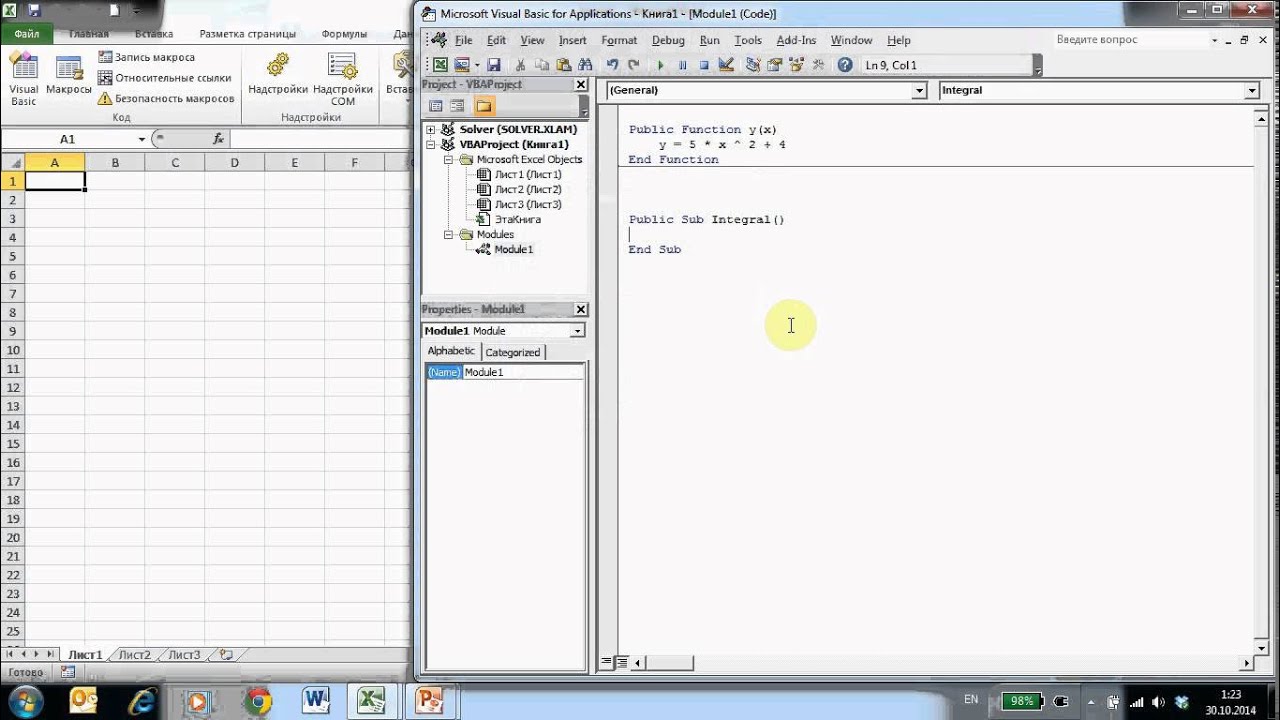
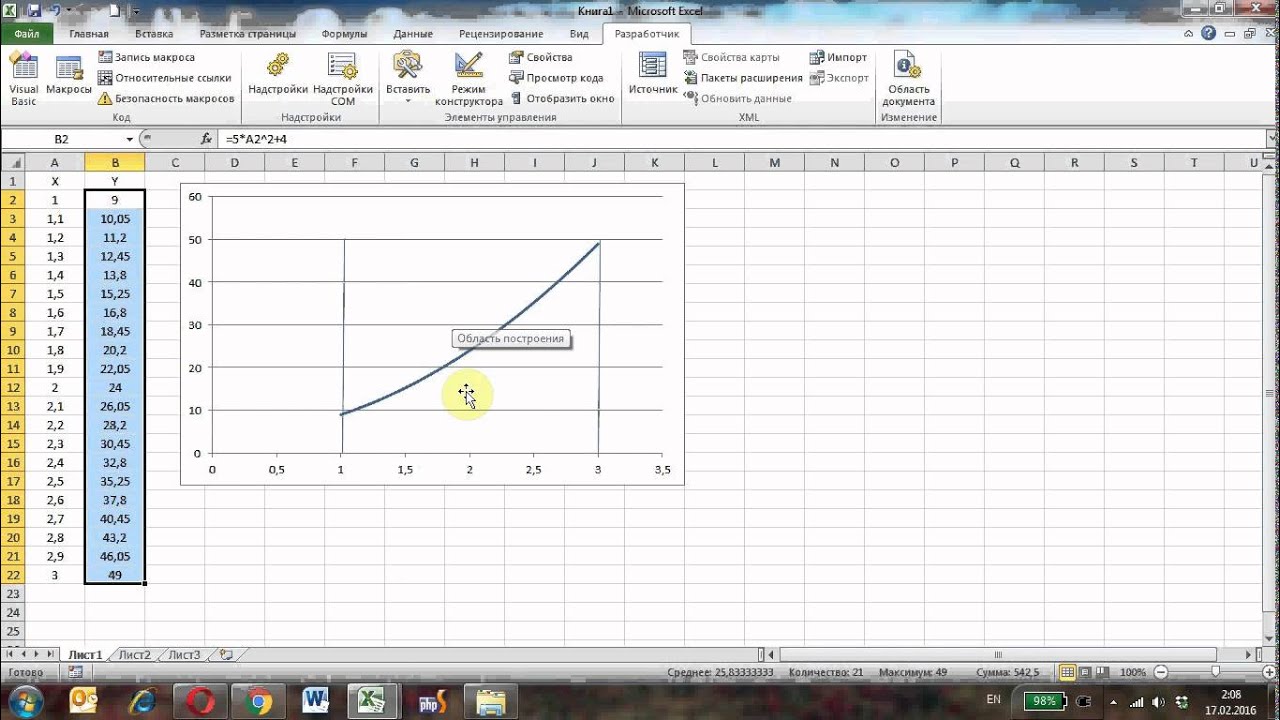
Кто учился в институте помнит, насколько сложной может быть задача вычисления определенного интеграла заданной функции. С помощью Microsoft Excel и численного метода трапеций данная задача решается гораздо проще и быстрее. Данный урок расскажет вам об этом.

Распространенным методом анализа товарного портфеля предприятия по критерию доходности является ABC-анализ. В нашем уроке мы напишем программу, которая выполняет его для любого количества товаров, введенного на рабочий лист Excel: к группе А программа относит наиболее доходные товары, к группе В - со средней доходностью, С - наименее успешные.

Скачать полученный в данном видеоуроке файл Excel можно по ссылке https://drive.google.com/open?....id=1iRsXZyA21w3ns2iN

С помощью Microsoft Excel у нас имеется возможность решать различные типы оптимизационных задач. Рассмотрим простейшую из них - задачу о распределении ресурсов. Воспользуемся при этом инструментом "Поиск решений" и, как всегда, создадим макрос, позволяющий автоматизировать указанный процесс и оценивать различные производственные ситуации.

В нашей подборке вы можете найти больше видеоуроков по работе с электронными таблицами Microsoft Excel:
http://bit.ly/2MecPWZ

Еще больше других обучающих видеоуроков вы сможете найти на нашем сайте: http://videolections.blogspot.com/

По вопросам сотрудничества - marcellidenumana@gmail.com

ПОДПИШИСЬ НА КАНАЛ - https://www.youtube.com/c/StudyProf

Буду благодарен за поддержку канала для улучшения контента!
Номер карты: 5375 4141 1409 0185

Мой Twitter - https://twitter.com/StudyProf_
Мой Instagram - https://www.instagram.com/study_prof/
Мой FB - https://www.facebook.com/StudyProf/

В данной ситуации требуется распределить имеющуюся денежную сумму инвестиционных вложений между тремя предприятиями так, чтобы ежегодная прибыль от этих вложений была как можно больше. Для решения этой задачи используем инструмент Excel - Поиск решений.

С помощью серии имитационных экспериментов можно успешно решать различные классы задач. В данном видеоуроке мы увидим, как можно найти площадь круга с помощью датчика случайных чисел Microsoft Excel.

При нахождении определенного интеграла сложных непрерывных функций современные аналитические методы не всегда могут помочь. На помощь приходят численные методы. В данном видеоуроке мы узнаем, как с помощью датчика случайных чисел и имитационного эксперимента в среде Excel, можно найти определенный интеграл заданной непрерывной функции

В данном видеоуроке мы будем учиться отыскивать кратчайший путь между двумя пунктами, соединенными между собой множеством различных маршрутов. Такая задача в теории графов называется задачей о кратчайшем пути. Для ее решения будем использовать Поиск решений Microsoft Excel.

В нашей подборке вы можете найти больше видеоуроков по работе с электронными таблицами Microsoft Excel:
http://bit.ly/2MecPWZ

Еще больше других обучающих видеоуроков вы сможете найти на нашем сайте: http://videolections.blogspot.com/

По вопросам сотрудничества - marcellidenumana@gmail.com

ПОДПИШИСЬ НА КАНАЛ - https://www.youtube.com/c/StudyProf

Буду благодарен за поддержку канала для улучшения контента!
Номер карты: 5375 4141 1409 0185

Мой Twitter - https://twitter.com/StudyProf_
Мой Instagram - https://www.instagram.com/study_prof/
Мой FB - https://www.facebook.com/StudyProf/

Решая в одном из последних видеоуроков задачу о кратчайшем пути, мы работали с ориентированным графом. То есть, дуги, связывающие вершины, имели направления. Ну а как быть, если граф не ориентирован, когда разрешено двигаться по дугам как в одном, так и в противоположном направлении? В этом видеоуроке я расскажу, какие изменения следует внести в исходные данные на рабочем листе, чтобы разрешить построение маршрута во всех направлениях.

Файл Excel, который используется в ролике, можно скачать по ссылке:
https://drive.google.com/file/....d/1r-yHzf9txSq-K2mJU

В нашей подборке вы сможете найти больше видеоуроков по работе с электронными таблицами Microsoft Excel:
http://bit.ly/2MecPWZ

Еще больше других обучающих видеоуроков вы сможете найти на нашем сайте: http://videolections.blogspot.com/

По вопросам сотрудничества - marcellidenumana@gmail.com

ПОДПИШИСЬ НА КАНАЛ - https://www.youtube.com/c/StudyProf

Буду благодарен за поддержку канала для улучшения контента!
Номер карты (грн.): 5375 4141 1409 0185
Номер карты (usd): 4731 1856 1771 3067

Мой Twitter - https://twitter.com/StudyProf_
Мой Instagram - https://www.instagram.com/study_prof/
Мой FB - https://www.facebook.com/StudyProf/

Не всегда можно решить задачу о кратчайшем пути Поиском решений Excel. Например, вершин у графа так много, что область изменяемых ячеек превышает допустимое их количество! В такой ситуации на помощь приходят специализированные алгоритмы. В нашем видеоуроке мы рассмотрим известный алгоритм Дейкстры и его практическое использование при решении задачи о кратчайшем пути.

Файл Excel с примером решения задачи вы можете скачать по ссылке:
https://drive.google.com/open?....id=1vDRb-fjhX19DVXSP

Производственная функция Кобба-Дугласа строится на основе исходных статистических данных о динамике выпуска продукции и использованных производственных факторах (основного капитала и трудовых ресурсов). В нашем видеоуроке мы последовательно рассмотрим процесс построения производственной функции в среде Excel.

Скачать файл Excel с расчетами вы можете по ссылке https://drive.google.com/open?....id=1kXljrIYCLUOEY1TZ

Прежде чем выполнять анализ эффективности использования ресурсов, построенная производственная функция должна быть проверена на адекватность исходным статистическим данным. В нашем видеоуроке мы будет использовать для этого критерий Фишера.

Построив по статистическим данным производственную функцию Кобба-Дугласа и оценив ее адекватность, переходим к показателям оценки эффективности ее ресурсов: средней эффективности, предельной эффективности, эластичности и нормы замещения

В этом видеоуроке мы будем на практике учиться рассчитывать показатели анализа производственной функции Кобба-Дугласа: среднюю и предельную эффективность ресурсов, эластичность и норму замещения.

Заключительным этапом анализа производственных функций является построение изоквант и изоклиналей. В данном видеоуроке мы дадим определение этим понятиям, приведем соответствующие формулы и рассмотрим на конкретном практическом примере весь процесс их построения.

Каждый из нас живет в условиях постоянных ограничений ресурсов: финансовых, материальных, временных. При этом, нам постоянно приходится выбирать, как распорядиться имеющимися ресурсами, чтобы выгода от их использования была как можно больше. Таким образом, мы постоянно, не задумываясь, на уровне интуиции решаем оптимизационные задачи. Кто-то справляется с этим лучше, а кто-то хуже. В математике выделилось целое направление - исследование операций или математическое программирование, которое изучает этапы построения оптимизационных моделей и методы их решений. В данном видеоуроке мы рассмотрим пример построения экономико-математической модели. А вопросами ее решения займемся позже.