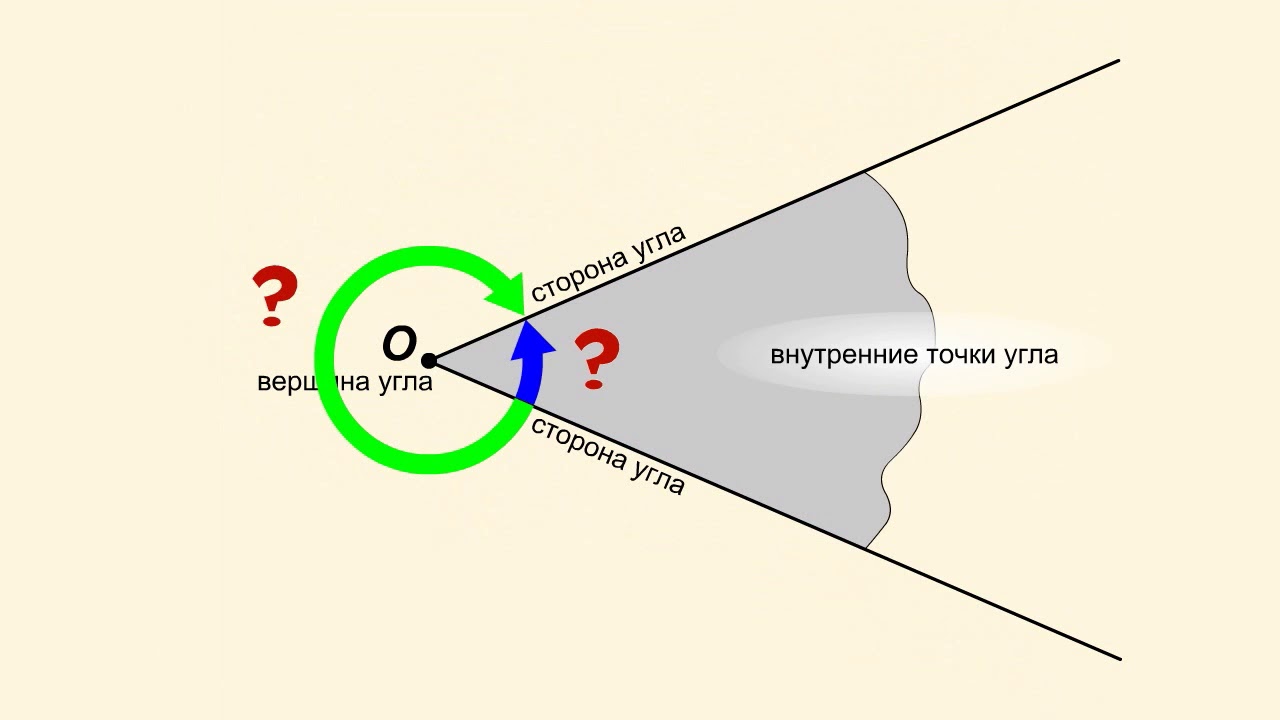
Биссектриса угла
Биссектрису угла также можно рассматривать как геометрическое место точек.
Докажем, что геометрическим местом точек, расположенных внутри данного угла и равноудаленных от его сторон, является биссектриса этого угла.
Проведем следующие рассуждения.
Первое рассуждение.
Если точка М расположена внутри угла и находится на равных расстояниях от его сторон, то М лежит на биссектрисе этого угла.
Доказательство.
Опустив перпендикуляры МА и МВ на стороны угла, из равенства МА = МВ на основании соответствующего признака равенства прямоугольных треугольников получим, что треугольники ОМА и ОМВ равны. Значит, равны углы МОА и МОВ, т.е. OM — биссектриса угла АОВ.
Второе рассуждение.
Если точка М лежит на биссектрисе, то М равноудалена от сторон угла.
Доказательство.
При симметрии относительно прямой, содержащей биссектрису, стороны угла перейдут друг в друга.
Напомним, что через любую точку плоскости проходит единственный перпендикуляр к заданной прямой.